Line integral

Template:Short description Template:More citations needed {{#invoke:sidebar|collapsible | class = plainlist | titlestyle = padding-bottom:0.25em; | pretitle = Part of a series of articles about | title = Calculus | image = $\underset{a}{\overset{b}{\int }}{f}^{\prime }(t)dt=f(b)-f(a)$ | listtitlestyle = text-align:center; | liststyle = border-top:1px solid #aaa;padding-top:0.15em;border-bottom:1px solid #aaa; | expanded = multivariable | abovestyle = padding:0.15em 0.25em 0.3em;font-weight:normal; | above =

• Fundamental theorem

• Limits
• Continuity

• Rolle's theorem
• Mean value theorem
• Inverse function theorem

| list2name = differential | list2titlestyle = display:block;margin-top:0.65em; | list2title = Template:Bigger | list2 ={{#invoke:sidebar|sidebar|child=yes

 |contentclass=hlist
 | heading1 = Definitions
 | content1 =

• Derivative (generalizations)
• Differential
  • infinitesimal
  • of a function
  • total

 | heading2 = Concepts
 | content2 =

• Differentiation notation
• Second derivative
• Implicit differentiation
• Logarithmic differentiation
• Related rates
• Taylor's theorem

 | heading3 = Rules and identities
 | content3 =

• Sum
• Product
• Chain
• Power
• Quotient
• L'Hôpital's rule
• Inverse
• General Leibniz
• Faà di Bruno's formula
• Reynolds

}}

| list3name = integral | list3title = Template:Bigger | list3 ={{#invoke:sidebar|sidebar|child=yes

 |contentclass=hlist
 | content1 =

• Lists of integrals
• Integral transform
• Leibniz integral rule

| heading2 = Definitions

 | content2 =

• Antiderivative
• Integral (improper)
• Riemann integral
• Lebesgue integration
• Contour integration
• Integral of inverse functions

 | heading3 = Integration by
 | content3 =

• Parts
• Discs
• Cylindrical shells
• Substitution (trigonometric, tangent half-angle, Euler)
• Euler's formula
• Partial fractions (Heaviside's method)
• Changing order
• Reduction formulae
• Differentiating under the integral sign
• Risch algorithm

}}

| list4name = series | list4title = Template:Bigger | list4 ={{#invoke:sidebar|sidebar|child=yes

 |contentclass=hlist
 | content1 =

• Geometric (arithmetico-geometric)
• Harmonic
• Alternating
• Power
• Binomial
• Taylor

 | heading2 = Convergence tests
 | content2 =

• Summand limit (term test)
• Ratio
• Root
• Integral
• Direct comparison
• 
  Limit comparison
• Alternating series
• Cauchy condensation
• Dirichlet
• Abel

}}

| list5name = vector | list5title = Template:Bigger | list5 ={{#invoke:sidebar|sidebar|child=yes

 |contentclass=hlist
 | content1 =

• Gradient
• Divergence
• Curl
• Laplacian
• Directional derivative
• Identities

 | heading2 = Theorems
 | content2 =

• Gradient
• Green's
• Stokes'
• Divergence
• generalized Stokes
• Helmholtz decomposition

}}

| list6name = multivariable | list6title = Template:Bigger | list6 ={{#invoke:sidebar|sidebar|child=yes

 |contentclass=hlist
 | heading1 = Formalisms
 | content1 =

• Matrix
• Tensor
• Exterior
• Geometric

 | heading2 = Definitions
 | content2 =

• Partial derivative
• Multiple integral
• Line integral
• Surface integral
• Volume integral
• Jacobian
• Hessian

}}

| list7name = advanced | list7title = Template:Bigger | list7 ={{#invoke:sidebar|sidebar|child=yes

 |contentclass=hlist
 | content1 =

• Calculus on Euclidean space
• Generalized functions
• Limit of distributions

}}

| list8name = specialized | list8title = Template:Bigger | list8 =

• Fractional
• Malliavin
• Stochastic
• Variations

| list9name = miscellanea | list9title = Template:Bigger | list9 =

• Precalculus
• History
• Glossary
• List of topics
• Integration Bee
• Mathematical analysis
• Nonstandard analysis

}}

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.

The function to be integrated may be a scalar field or a vector field. The value of the line integral is the sum of values of the field at all points on the curve, weighted by some scalar function on the curve (commonly arc length or, for a vector field, the scalar product of the vector field with a differential vector in the curve). This weighting distinguishes the line integral from simpler integrals defined on intervals. Many simple formulae in physics, such as the definition of work as Template:Nowrap have natural continuous analogues in terms of line integrals, in this case Template:Nowrap which computes the work done on an object moving through an electric or gravitational field Template:Math along a path Template:Nowrap

Vector calculus

In qualitative terms, a line integral in vector calculus can be thought of as a measure of the total effect of a given tensor field along a given curve. For example, the line integral over a scalar field (rank 0 tensor) can be interpreted as the area under the field carved out by a particular curve. This can be visualized as the surface created by Template:Math and a curve C in the xy plane. The line integral of f would be the area of the "curtain" created—when the points of the surface that are directly over C are carved out.

Line integral of a scalar field

The line integral over a scalar field f can be thought of as the area under the curve C along a surface Template:Math, described by the field.

Definition

For some scalar field $f:U\to ℝ$ where $U\subseteq {ℝ}^n$, the line integral along a piecewise smooth curve $𝒞\subset U$ is defined as $$\underset{𝒞}{\int }fds=\underset{a}{\overset{b}{\int }}f(𝐫(t))|{𝐫}^{\prime }(t)|dt,$$ where $𝐫:[a,b]\to 𝒞$ is an arbitrary bijective parametrization of the curve $𝒞$ such that Template:Math and Template:Math give the endpoints of $𝒞$ and Template:Math. Here, and in the rest of the article, the absolute value bars denote the standard (Euclidean) norm of a vector.

The function Template:Mvar is called the integrand, the curve $𝒞$ is the domain of integration, and the symbol Template:Math may be intuitively interpreted as an elementary arc length of the curve $𝒞$ (i.e., a differential length of $𝒞$). Line integrals of scalar fields over a curve $𝒞$ do not depend on the chosen parametrization Template:Math of $𝒞$.

Geometrically, when the scalar field Template:Mvar is defined over a plane Template:Math, its graph is a surface Template:Math in space, and the line integral gives the (signed) cross-sectional area bounded by the curve $𝒞$ and the graph of Template:Mvar. See the animation to the right.

Derivation

For a line integral over a scalar field, the integral can be constructed from a Riemann sum using the above definitions of Template:Mvar, Template:Mvar and a parametrization Template:Math of Template:Mvar. This can be done by partitioning the interval Template:Math into Template:Mvar sub-intervals Template:Math of length Template:Math, then Template:Math denotes some point, call it a sample point, on the curve Template:Mvar. We can use the set of sample points Template:Math to approximate the curve Template:Mvar as a polygonal path by introducing the straight line piece between each of the sample points Template:Math and Template:Math. (The approximation of a curve to a polygonal path is called rectification of a curve, see here for more details.) We then label the distance of the line segment between adjacent sample points on the curve as Template:Math. The product of Template:Math and Template:Math can be associated with the signed area of a rectangle with a height and width of Template:Math and Template:Math, respectively. Taking the limit of the sum of the terms as the length of the partitions approaches zero gives us $$I=\underset{\mathrm{\Delta }{s}_i\to 0}{\lim }\sum _{i=1}^{n}f(𝐫(t_i))\mathrm{\Delta }{s}_i.$$

By the mean value theorem, the distance between subsequent points on the curve, is $$\mathrm{\Delta }{s}_i=|𝐫(t_i+\mathrm{\Delta }t)-𝐫(t_i)|\approx |{𝐫}^{\prime }(t_i)\mathrm{\Delta }t|$$

Substituting this in the above Riemann sum yields $$I=\underset{\mathrm{\Delta }t\to 0}{\lim }\sum _{i=1}^{n}f(𝐫(t_i))|{𝐫}^{\prime }(t_i)|\mathrm{\Delta }t$$ which is the Riemann sum for the integral $$I=\underset{a}{\overset{b}{\int }}f(𝐫(t))|{𝐫}^{\prime }(t)|dt.$$

Line integral of a vector field

Definition

For a vector field Template:Math, the line integral along a piecewise smooth curve Template:Math, in the direction of r, is defined as $$\underset{C}{\int }𝐅(𝐫)\cdot d𝐫=\underset{a}{\overset{b}{\int }}𝐅(𝐫(t))\cdot {𝐫}^{\prime }(t)dt$$ where Template:Math is the dot product, and Template:Math is a regular parametrization (i.e: $||{𝐫}^{\prime }(t)||\ne 0\mathrm{\forall }t\in [a,b]$) of the curve C such that Template:Math and Template:Math give the endpoints of C.

A line integral of a scalar field is thus a line integral of a vector field, where the vectors are always tangential to the line of the integration.

Line integrals of vector fields are independent of the parametrization r in absolute value, but they do depend on its orientation. Specifically, a reversal in the orientation of the parametrization changes the sign of the line integral.

From the viewpoint of differential geometry, the line integral of a vector field along a curve is the integral of the corresponding 1-form under the musical isomorphism (which takes the vector field to the corresponding covector field), over the curve considered as an immersed 1-manifold.

Derivation

The trajectory of a particle (in red) along a curve inside a vector field. Starting from a, the particle traces the path C along the vector field F. The dot product (green line) of its tangent vector (red arrow) and the field vector (blue arrow) defines an area under a curve, which is equivalent to the path's line integral. (Click on image for a detailed description.)

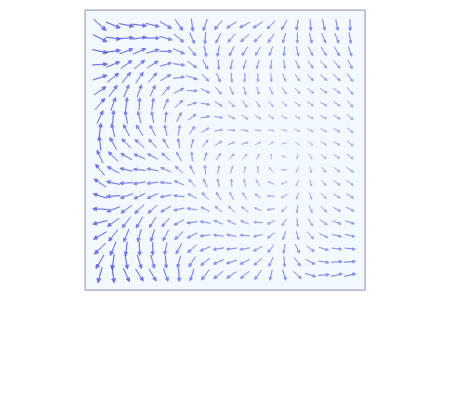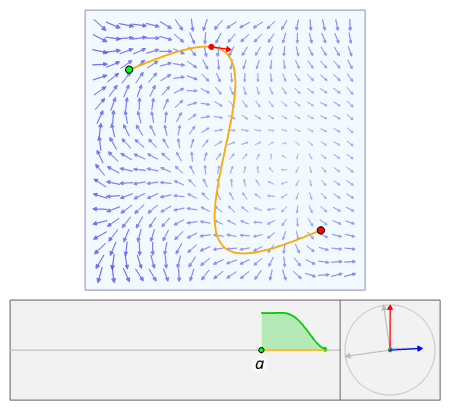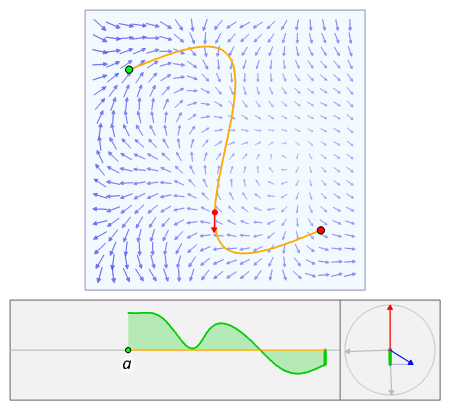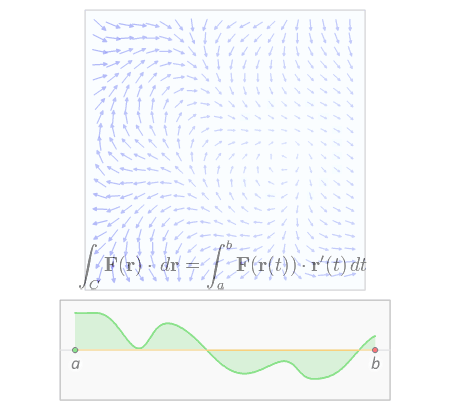
The line integral of a vector field can be derived in a manner very similar to the case of a scalar field, but this time with the inclusion of a dot product. Again using the above definitions of Template:Math, Template:Mvar and its parametrization Template:Math, we construct the integral from a Riemann sum. We partition the interval Template:Math (which is the range of the values of the parameter Template:Mvar) into Template:Mvar intervals of length Template:Math. Letting Template:Math be the Template:Mvarth point on Template:Math, then Template:Math gives us the position of the Template:Mvarth point on the curve. However, instead of calculating up the distances between subsequent points, we need to calculate their displacement vectors, Template:Math. As before, evaluating Template:Math at all the points on the curve and taking the dot product with each displacement vector gives us the infinitesimal contribution of each partition of Template:Math on Template:Mvar. Letting the size of the partitions go to zero gives us a sum $$I=\underset{\mathrm{\Delta }t\to 0}{\lim }\sum _{i=1}^n𝐅(𝐫(t_i))\cdot \mathrm{\Delta }{𝐫}_i$$

By the mean value theorem, we see that the displacement vector between adjacent points on the curve is $$\mathrm{\Delta }{𝐫}_i=𝐫(t_i+\mathrm{\Delta }t)-𝐫(t_i)\approx {𝐫}^{\prime }(t_i)\mathrm{\Delta }t.$$

Substituting this in the above Riemann sum yields $$I=\underset{\mathrm{\Delta }t\to 0}{\lim }\sum _{i=1}^n𝐅(𝐫(t_i))\cdot {𝐫}^{\prime }(t_i)\mathrm{\Delta }t,$$

which is the Riemann sum for the integral defined above.

Path independence

If a vector field Template:Math is the gradient of a scalar field Template:Math (i.e. if Template:Math is conservative), that is, $$𝐅=\mathrm{\nabla }G,$$ then by the multivariable chain rule the derivative of the composition of Template:Math and Template:Math is $$\frac{dG(𝐫(t))}{dt}=\mathrm{\nabla }G(𝐫(t))\cdot {𝐫}^{\prime }(t)=𝐅(𝐫(t))\cdot {𝐫}^{\prime }(t)$$ which happens to be the integrand for the line integral of Template:Math on Template:Math. It follows, given a path C, that $$\underset{C}{\int }𝐅(𝐫)\cdot d𝐫=\underset{a}{\overset{b}{\int }}𝐅(𝐫(t))\cdot {𝐫}^{\prime }(t)dt=\underset{a}{\overset{b}{\int }}\frac{dG(𝐫(t))}{dt}dt=G(𝐫(b))-G(𝐫(a)).$$

In other words, the integral of Template:Math over C depends solely on the values of Template:Math at the points Template:Math and Template:Math, and is thus independent of the path between them. For this reason, a line integral of a conservative vector field is called path independent.

Applications

The line integral has many uses in physics. For example, the work done on a particle traveling on a curve C inside a force field represented as a vector field Template:Math is the line integral of Template:Math on C.

Flow across a curve

For a vector field $𝐅:U\subseteq {ℝ}^2\to {ℝ}^2$, Template:Math, the line integral across a curve C ⊂ U, also called the flux integral, is defined in terms of a piecewise smooth parametrization Template:Math, Template:Math, as: $$\underset{C}{\int }𝐅(𝐫)\cdot d{𝐫}^{\perp }=\underset{a}{\overset{b}{\int }}\left[\begin{array}{c}P(x(t),y(t))\\ Q(x(t),y(t))\end{array}\right]\cdot \left[\begin{array}{c}{y}^{\prime }(t)\\ -x^{\prime }(t)\end{array}\right]dt=\underset{a}{\overset{b}{\int }}(-Qdx+Pdy).$$

Here Template:Math is the dot product, and ${𝐫}^{\prime }(t{)}^{\perp }=(y^{\prime }(t),-x^{\prime }(t))$ is the clockwise perpendicular of the velocity vector Template:Nowrap

The flow is computed in an oriented sense: the curve Template:Mvar has a specified forward direction from Template:Math to Template:Math, and the flow is counted as positive when Template:Math is on the clockwise side of the forward velocity vector Template:Math.

Complex line integral

In complex analysis, the line integral is defined in terms of multiplication and addition of complex numbers. Suppose U is an open subset of the complex plane C, Template:Math is a function, and $L\subset U$ is a curve of finite length, parametrized by Template:Math, where Template:Math. The line integral $$\underset{L}{\int }f(z)dz$$ may be defined by subdividing the interval [a, b] into Template:Nowrap and considering the expression $$\sum _{k=1}^{n}f(\gamma (t_k))[\gamma (t_k)-\gamma (t_{k-1})]=\sum _{k=1}^{n}f({\gamma }_k)\mathrm{\Delta }{\gamma }_k.$$

The integral is then the limit of this Riemann sum as the lengths of the subdivision intervals approach zero.

If the parametrization Template:Mvar is continuously differentiable, the line integral can be evaluated as an integral of a function of a real variable: $$\underset{L}{\int }f(z)dz=\underset{a}{\overset{b}{\int }}f(\gamma (t)){\gamma }^{\prime }(t)dt.$$

When Template:Mvar is a closed curve (initial and final points coincide), the line integral is often denoted ${\oint }_{L}f(z)dz,$ sometimes referred to in engineering as a cyclic integral.

To establish a complete analogy with the line integral of a vector field, one must go back to the definition of differentiability in multivariable calculus. The gradient is defined from Riesz representation theorem, and inner products in complex analysis involve conjugacy (the gradient of a function $\gamma$ at some $z\in ℂ$ would be $\overline{{\gamma }^{\prime }(z)}$, and the complex inner product would attribute twice a conjugate to ${\gamma }^{\prime }$ in the vector field definition of a line integral).

The line integral with respect to the conjugate complex differential $\overline{dz}$ is defined to be $$\underset{L}{\int }f(z)\overline{dz}:=\overline{\underset{L}{\int }\stackrel{‾}{f(z)}dz}=\underset{a}{\overset{b}{\int }}f(\gamma (t))\overline{{\gamma }^{\prime }(t)}dt.$$

The line integrals of complex functions can be evaluated using a number of techniques. The most direct is to split into real and imaginary parts, reducing the problem to evaluating two real-valued line integrals. The Cauchy integral theorem may be used to equate the line integral of an analytic function to the same integral over a more convenient curve. It also implies that over a closed curve enclosing a region where Template:Math is analytic without singularities, the value of the integral is simply zero, or in case the region includes singularities, the residue theorem computes the integral in terms of the singularities. This also implies the path independence of complex line integral for analytic functions.

Example

Consider the function Template:Math, and let the contour L be the counterclockwise unit circle about 0, parametrized by Template:Math with Template:Mvar in Template:Math using the complex exponential. Substituting, we find: $$\begin{array}{cc}{\oint }_L\frac{1}{z}dz& =\underset{0}{\overset{2\pi }{\int }}\frac{1}{e^{it}}i{e}^{it}dt=i\underset{0}{\overset{2\pi }{\int }}{e}^{-it}{e}^{it}dt\\ & =i\underset{0}{\overset{2\pi }{\int }}dt=i(2\pi -0)=2\pi i.\end{array}$$

This is a typical result of Cauchy's integral formula and the residue theorem.

Relation of complex line integral and line integral of vector field

Viewing complex numbers as 2-dimensional vectors, the line integral of a complex-valued function $f(z)$ has real and complex parts equal to the line integral and the flux integral of the vector field corresponding to the conjugate function $\overline{f(z)}.$ Specifically, if $𝐫(t)=(x(t),y(t))$ parametrizes L, and $f(z)=u(z)+iv(z)$ corresponds to the vector field $𝐅(x,y)=\overline{f(x+iy)}=(u(x+iy),-v(x+iy)),$ then: $$\begin{array}{cc}\underset{L}{\int }f(z)dz& =\underset{L}{\int }(u+iv)(dx+idy)\\ & =\underset{L}{\int }(u,-v)\cdot (dx,dy)+i\underset{L}{\int }(u,-v)\cdot (dy,-dx)\\ & =\underset{L}{\int }𝐅(𝐫)\cdot d𝐫+i\underset{L}{\int }𝐅(𝐫)\cdot d{𝐫}^{\perp }.\end{array}$$

By Cauchy's theorem, the left-hand integral is zero when $f(z)$ is analytic (satisfying the Cauchy–Riemann equations) for any smooth closed curve L. Correspondingly, by Green's theorem, the right-hand integrals are zero when $𝐅=\overline{f(z)}$ is irrotational (curl-free) and incompressible (divergence-free). In fact, the Cauchy-Riemann equations for $f(z)$ are identical to the vanishing of curl and divergence for Template:Math.

By Green's theorem, the area of a region enclosed by a smooth, closed, positively oriented curve $L$ is given by the integral $\frac{1}{2i}\underset{L}{\int }\bar{z}dz.$ This fact is used, for example, in the proof of the area theorem.

Quantum mechanics

The path integral formulation of quantum mechanics actually refers not to path integrals in this sense but to functional integrals, that is, integrals over a space of paths, of a function of a possible path. However, path integrals in the sense of this article are important in quantum mechanics; for example, complex contour integration is often used in evaluating probability amplitudes in quantum scattering theory.

See also

• Divergence theorem
• Gradient theorem
• Methods of contour integration
• Nachbin's theorem
• Line element
• Surface integral
• Volume element
• Volume integral

External links

• Template:Springer
• Khan Academy modules:
  • "Introduction to the Line Integral"
  • "Line Integral Example 1"
  • "Line Integral Example 2 (part 1)"
  • "Line Integral Example 2 (part 2)"
• Template:PlanetMath
• Line integral of a vector field – Interactive