Order-6 tetrahedral honeycomb

Order-6 tetrahedral honeycomb
Perspective projection view within Poincaré disk model
Type	Hyperbolic regular honeycomb Paracompact uniform honeycomb
Schläfli symbols	{3,3,6} {3,3[3]}
Coxeter diagrams	Template:CDD Template:CDD ↔ Template:CDD
Cells	{3,3}
Faces	triangle {3}
Edge figure	hexagon {6}
Vertex figure	triangular tiling
Dual	Hexagonal tiling honeycomb
Coxeter groups	${\bar{V}}_3$, [3,3,6] ${\bar{P}}_3$, [3,3[3]]
Properties	Regular, quasiregular

In hyperbolic 3-space, the order-6 tetrahedral honeycomb is a paracompact regular space-filling tessellation (or honeycomb). It is paracompact because it has vertex figures composed of an infinite number of faces, and has all vertices as ideal points at infinity. With Schläfli symbol {3,3,6}, the order-6 tetrahedral honeycomb has six ideal tetrahedra around each edge. All vertices are ideal, with infinitely many tetrahedra existing around each vertex in a triangular tiling vertex figure.

Symmetry constructions

Subgroup relations

The order-6 tetrahedral honeycomb has a second construction as a uniform honeycomb, with Schläfli symbol {3,3^[3]}. This construction contains alternating types, or colors, of tetrahedral cells. In Coxeter notation, this half symmetry is represented as [3,3,6,1⁺] ↔ [3,((3,3,3))], or [3,3^[3]]: Template:CDD ↔ Template:CDD.

Related polytopes and honeycombs

The order-6 tetrahedral honeycomb is analogous to the two-dimensional infinite-order triangular tiling, {3,∞}. Both tessellations are regular, and only contain triangles and ideal vertices.

The order-6 tetrahedral honeycomb is also a regular hyperbolic honeycomb in 3-space, and one of 11 which are paracompact. Template:Regular paracompact H3 honeycombs

This honeycomb is one of 15 uniform paracompact honeycombs in the [6,3,3] Coxeter group, along with its dual, the hexagonal tiling honeycomb. Template:633 family

The order-6 tetrahedral honeycomb is part of a sequence of regular polychora and honeycombs with tetrahedral cells. Template:Tetrahedral cell tessellations

It is also part of a sequence of honeycombs with triangular tiling vertex figures. Template:Triangular tiling vertex figure tessellations

Rectified order-6 tetrahedral honeycomb

Rectified order-6 tetrahedral honeycomb
Type	Paracompact uniform honeycomb Semiregular honeycomb
Schläfli symbols	r{3,3,6} or t1{3,3,6}
Coxeter diagrams	Template:CDD Template:CDD ↔ Template:CDD
Cells	r{3,3} {3,6}
Faces	triangle {3}
Vertex figure	hexagonal prism
Coxeter groups	${\bar{V}}_3$, [3,3,6] ${\bar{P}}_3$, [3,3[3]]
Properties	Vertex-transitive, edge-transitive

The rectified order-6 tetrahedral honeycomb, t₁{3,3,6} has octahedral and triangular tiling cells arranged in a hexagonal prism vertex figure.

Perspective projection view within Poincaré disk model

Truncated order-6 tetrahedral honeycomb

Truncated order-6 tetrahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	t{3,3,6} or t0,1{3,3,6}
Coxeter diagrams	Template:CDD Template:CDD ↔ Template:CDD
Cells	t{3,3} {3,6}
Faces	triangle {3} hexagon {6}
Vertex figure	hexagonal pyramid
Coxeter groups	${\bar{V}}_3$, [3,3,6] ${\bar{P}}_3$, [3,3[3]]
Properties	Vertex-transitive

The truncated order-6 tetrahedral honeycomb, t_0,1{3,3,6} has truncated tetrahedron and triangular tiling cells arranged in a hexagonal pyramid vertex figure.

Bitruncated order-6 tetrahedral honeycomb

The bitruncated order-6 tetrahedral honeycomb is equivalent to the bitruncated hexagonal tiling honeycomb.

Cantellated order-6 tetrahedral honeycomb

Cantellated order-6 tetrahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	rr{3,3,6} or t0,2{3,3,6}
Coxeter diagrams	Template:CDD Template:CDD ↔ Template:CDD
Cells	r{3,3} r{3,6} {}x{6}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	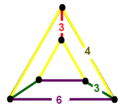isosceles triangular prism
Coxeter groups	${\bar{V}}_3$, [3,3,6] ${\bar{P}}_3$, [3,3[3]]
Properties	Vertex-transitive

The cantellated order-6 tetrahedral honeycomb, t_0,2{3,3,6} has cuboctahedron, trihexagonal tiling, and hexagonal prism cells arranged in an isosceles triangular prism vertex figure.

Cantitruncated order-6 tetrahedral honeycomb

Cantitruncated order-6 tetrahedral honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	tr{3,3,6} or t0,1,2{3,3,6}
Coxeter diagrams	Template:CDD Template:CDD ↔ Template:CDD
Cells	tr{3,3} t{3,6} {}x{6}
Faces	square {4} hexagon {6}
Vertex figure	mirrored sphenoid
Coxeter groups	${\bar{V}}_3$, [3,3,6] ${\bar{P}}_3$, [3,3[3]]
Properties	Vertex-transitive

The cantitruncated order-6 tetrahedral honeycomb, t_0,1,2{3,3,6} has truncated octahedron, hexagonal tiling, and hexagonal prism cells connected in a mirrored sphenoid vertex figure.

Runcinated order-6 tetrahedral honeycomb

The bitruncated order-6 tetrahedral honeycomb is equivalent to the bitruncated hexagonal tiling honeycomb.

Runcitruncated order-6 tetrahedral honeycomb

The runcitruncated order-6 tetrahedral honeycomb is equivalent to the runcicantellated hexagonal tiling honeycomb.

Runcicantellated order-6 tetrahedral honeycomb

The runcicantellated order-6 tetrahedral honeycomb is equivalent to the runcitruncated hexagonal tiling honeycomb.

Omnitruncated order-6 tetrahedral honeycomb

The omnitruncated order-6 tetrahedral honeycomb is equivalent to the omnitruncated hexagonal tiling honeycomb.

See also

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space
• Paracompact uniform honeycombs

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. Template:Isbn. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, Template:LCCN, Template:Isbn (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
• Jeffrey R. Weeks The Shape of Space, 2nd edition Template:Isbn (Chapter 16-17: Geometries on Three-manifolds I, II)
• Norman Johnson Uniform Polytopes, Manuscript
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • N.W. Johnson: Geometries and Transformations, (2018) Chapter 13: Hyperbolic Coxeter groups