Triangular prism

Template:Short description Template:For

Template:Infobox polyhedron In geometry, a triangular prism or trigonal prismTemplate:Sfnp is a prism with 2 triangular bases. If the edges pair with each triangle's vertex and if they are perpendicular to the base, it is a right triangular prism. A right triangular prism may be both semiregular and uniform.

The triangular prism can be used in constructing another polyhedron. Examples are some of the Johnson solids, the truncated right triangular prism, and Schönhardt polyhedron.

Properties

A triangular prism has 6 vertices, 9 edges, and 5 faces. Every prism has 2 congruent faces known as its bases, and the bases of a triangular prism are triangles. The triangle has 3 vertices, each of which pairs with another triangle's vertex, making up another 3 edges. These edges form 3 parallelograms as other faces.^[1] If the prism's edges are perpendicular to the base, the lateral faces are rectangles, and the prism is called a right triangular prism.Template:Sfnp This prism may also be considered a special case of a wedge.Template:Sfnp

File:Triangular prism.stl If the base is equilateral and the lateral faces are square, then the right triangular prism is semiregular. A semiregular prism means that the number of its polygonal base's edges equals the number of its square faces.Template:Sfnp More generally, the triangular prism is uniform. This means that a triangular prism has regular faces and has an isogonal symmetry on vertices.^[2] The three-dimensional symmetry group of a right triangular prism is dihedral group Template:Math of order 12: the appearance is unchanged if the triangular prism is rotated one- and two- thirds of a full angle around its axis of symmetry passing through the center's base, and reflecting across a horizontal plane. The dual polyhedron of a triangular prism is a triangular bipyramid. The triangular bipyramid has the same symmetry as the triangular prism.Template:Sfnp The dihedral angle between two adjacent square faces is the internal angle of an equilateral triangle Template:Nowrap, and that between a square and a triangle is Template:Nowrap.Template:Sfnp

The volume of any prism is the product of the area of the base and the distance between the two bases.Template:Sfnp In the case of a triangular prism, its base is a triangle, so its volume can be calculated by multiplying the area of a triangle and the length of the prism: $\frac{b h l}{2},$ where Template:Mvar is the length of one side of the triangle, Template:Mvar is the length of an altitude drawn to that side, and Template:Mvar is the distance between the triangular faces.^[3] In the case of a right triangular prism, where all its edges are equal in length Template:Math, its volume can be calculated as the product of the equilateral triangle's area and length Template:Math:Template:Sfnp $\frac{\sqrt{3}}{2} l^{2} \cdot l \approx 0.433 l^{3}$

The triangular prism can be represented as the prism graph Template:Nowrap. More generally, the prism graph Template:Nowrap represents the Template:Nowrapsided prism.Template:Sfnp

Related polyhedron

In construction of polyhedron

Beyond the triangular bipyramid as its dual polyhedron, many other polyhedrons are related to the triangular prism. A Johnson solid is a convex polyhedron with regular faces, and this definition is sometimes omitted uniform polyhedrons such as Archimedean solids, Catalan solids, prisms and antiprisms.^[4] There are 6 Johnson solids with their construction involving the triangular prism: elongated triangular pyramid, elongated triangular bipyramid, gyrobifastigium, augmented triangular prism, biaugmented triangular prism, and triaugmented triangular prism. The elongated triangular pyramid and the gyroelongated triangular pyramid are constructed by attaching tetrahedron onto the base of a triangular prism. The augmented triangular prism, biaugmented triangular prism, and triaugmented triangular prism are constructed by attaching equilateral square pyramids onto the square face of the prism. The gyrobifastigium is constructed by attaching two triangular prisms along one of its square faces.^[5]

File:TruncatedTriangularPrism.png

Truncated right triangular prism

A truncated triangular prism is a triangular prism constructed by truncating its part at an oblique angle. As a result, the two bases are not parallel and every height has a different edge length. If the edges connecting bases are perpendicular to one of its bases, the prism is called a truncated right triangular prism. Given that Template:Math is the area of the triangular prism's base, and the three heights Template:Math, Template:Math, and Template:Math, its volume can be determined in the following formula:Template:Sfnp $\frac{A (h_{1} + h_{2} + h_{3})}{3} .$

Error creating thumbnail:

Schönhardt polyhedron

Schönhardt polyhedron is another polyhedron constructed from a triangular prism with equilateral triangle bases. This way, one of its bases rotates around the prism's centerline and breaks the square faces into skew polygons. Each square face can be re-triangulated with two triangles to form a non-convex dihedral angle.^[6] As a result, the Schönhardt polyhedron cannot be triangulated by a partition into tetrahedra. It is also that the Schönhardt polyhedron has no internal diagonals.Template:Sfnp It is named after German mathematician Erich Schönhardt, who described it in 1928, although the related structure was exhibited by artist Karlis Johansons Template:Nowrap

File:Crossed-triangular prism.png

A crossed triangular antiprism shares its vertex arrangement with a triangular prism as a faceting, with lateral isosceles triangles.

There are 4 uniform compounds of triangular prisms. They are compound of four triangular prisms, compound of eight triangular prisms, compound of ten triangular prisms, compound of twenty triangular prisms.Template:Sfnp

Honeycombs

There are 9 uniform honeycombs that include triangular prism cells:

Gyroelongated alternated cubic honeycomb, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb

Related polytopes

The triangular prism is first in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the triangular prism). In Coxeter's notation the triangular prism is given the symbol −1₂₁. Template:Gosset semiregular polytopes

Four dimensional space

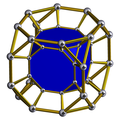
The triangular prism exists as cells of a number of four-dimensional uniform 4-polytopes, including:

Four dimensional polytopes with triangular prisms
Tetrahedral prism Template:CDD	Octahedral prism Template:CDD	Cuboctahedral prism Template:CDD	Icosahedral prism Template:CDD	Icosidodecahedral prism Template:CDD	Truncated dodecahedral prism Template:CDD
File:Tetrahedral prism.png	File:Octahedral prism.png	File:Cuboctahedral prism.png	Error creating thumbnail:
Rhomb-icosidodecahedral prism Template:CDD	Rhombi-cuboctahedral prism Template:CDD	Truncated cubic prism Template:CDD	Snub dodecahedral prism Template:CDD	n-gonal antiprismatic prism Template:CDD
Error creating thumbnail:
Cantellated 5-cell Template:CDD	Cantitruncated 5-cell Template:CDD	Runcinated 5-cell Template:CDD	Runcitruncated 5-cell Template:CDD	Cantellated tesseract Template:CDD	Cantitruncated tesseract Template:CDD	Runcinated tesseract Template:CDD	Runcitruncated tesseract Template:CDD
Error creating thumbnail:		File:4-simplex t03.svg		Error creating thumbnail:	File:4-cube t012.svg	File:4-cube t03.svg	Error creating thumbnail:
Cantellated 24-cell Template:CDD	Cantitruncated 24-cell Template:CDD	Runcinated 24-cell Template:CDD	Runcitruncated 24-cell Template:CDD	Cantellated 120-cell Template:CDD	Cantitruncated 120-cell Template:CDD	Runcinated 120-cell Template:CDD	Runcitruncated 120-cell Template:CDD
Error creating thumbnail:	File:24-cell t012 F4.svg	File:24-cell t03 F4.svg	File:24-cell t013 F4.svg	File:120-cell t02 H3.png	File:120-cell t012 H3.png	File:120-cell t03 H3.png	Error creating thumbnail: