Icosahedral honeycomb

Icosahedral honeycomb
Poincaré disk model
Type	Hyperbolic regular honeycomb Uniform hyperbolic honeycomb
Schläfli symbol	Template:Math
Coxeter diagram	Template:CDD
Cells	Template:Math (regular icosahedron)
Faces	Template:Math (triangle)
Edge figure	Template:Math (triangle)
Vertex figure	dodecahedron
Dual	Self-dual
Coxeter group	Template:Math
Properties	Regular

In geometry, the icosahedral honeycomb is one of four compact, regular, space-filling tessellations (or honeycombs) in hyperbolic 3-space. With Schläfli symbol Template:Math there are three icosahedra around each edge, and 12 icosahedra around each vertex, in a regular dodecahedral vertex figure. It is analogous to the 24-cell and the 5-cell.

Description

The dihedral angle of a regular icosahedron is around 138.2°, so it is impossible to fit three icosahedra around an edge in Euclidean 3-space. However, in hyperbolic space, properly scaled icosahedra can have dihedral angles of exactly 120 degrees, so three of those can fit around an edge.

Honeycomb seen in perspective outside Poincare's model disk

Related regular honeycombs

There are four regular compact honeycombs in 3D hyperbolic space: Template:Regular compact H3 honeycombs

Related regular polytopes and honeycombs

It is a member of a sequence of regular polychora and honeycombs {3,p,3} with deltrahedral cells: Template:Symmetric tessellations

It is also a member of a sequence of regular polychora and honeycombs {p,5,p}, with vertex figures composed of pentagons: Template:Symmetric4 tessellations

Uniform honeycombs

There are nine uniform honeycombs in the [3,5,3] Coxeter group family, including this regular form as well as the bitruncated form, t_1,2{3,5,3}, Template:CDD, also called truncated dodecahedral honeycomb, each of whose cells are truncated dodecahedra. Template:353 family

Rectified icosahedral honeycomb

Rectified icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	r{3,5,3} or t1{3,5,3}
Coxeter diagram	Template:CDD
Cells	r{3,5} {5,3}
Faces	triangle {3} pentagon {5}
Vertex figure	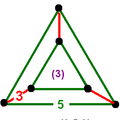triangular prism
Coxeter group	${\bar{J}}_3$, [3,5,3]
Properties	Vertex-transitive, edge-transitive

The rectified icosahedral honeycomb, t₁{3,5,3}, Template:CDD, has alternating dodecahedron and icosidodecahedron cells, with a triangular prism vertex figure:

Perspective projections from center of Poincaré disk model

Related honeycomb

There are four rectified compact regular honeycombs: Template:Rectified compact H3 honeycombs Template:Clear

Truncated icosahedral honeycomb

Truncated icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t{3,5,3} or t0,1{3,5,3}
Coxeter diagram	Template:CDD
Cells	t{3,5} {5,3}
Faces	pentagon {5} hexagon {6}
Vertex figure	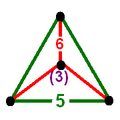triangular pyramid
Coxeter group	${\bar{J}}_3$, [3,5,3]
Properties	Vertex-transitive

The truncated icosahedral honeycomb, t_0,1{3,5,3}, Template:CDD, has alternating dodecahedron and truncated icosahedron cells, with a triangular pyramid vertex figure.

Bitruncated icosahedral honeycomb

Bitruncated icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	2t{3,5,3} or t1,2{3,5,3}
Coxeter diagram	Template:CDD
Cells	t{5,3}
Faces	triangle {3} decagon {10}
Vertex figure	tetragonal disphenoid
Coxeter group	$2\times {\bar{J}}_3$, [[3,5,3]]
Properties	Vertex-transitive, edge-transitive, cell-transitive

The bitruncated icosahedral honeycomb, t_1,2{3,5,3}, Template:CDD, has truncated dodecahedron cells with a tetragonal disphenoid vertex figure.

Cantellated icosahedral honeycomb

Cantellated icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	rr{3,5,3} or t0,2{3,5,3}
Coxeter diagram	Template:CDD
Cells	rr{3,5} r{5,3} {}x{3}
Faces	triangle {3} square {4} pentagon {5}
Vertex figure	wedge
Coxeter group	${\bar{J}}_3$, [3,5,3]
Properties	Vertex-transitive

The cantellated icosahedral honeycomb, t_0,2{3,5,3}, Template:CDD, has rhombicosidodecahedron, icosidodecahedron, and triangular prism cells, with a wedge vertex figure.

Cantitruncated icosahedral honeycomb

Cantitruncated icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	tr{3,5,3} or t0,1,2{3,5,3}
Coxeter diagram	Template:CDD
Cells	tr{3,5} t{5,3} {}x{3}
Faces	triangle {3} square {4} hexagon {6} decagon {10}
Vertex figure	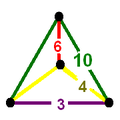mirrored sphenoid
Coxeter group	${\bar{J}}_3$, [3,5,3]
Properties	Vertex-transitive

The cantitruncated icosahedral honeycomb, t_0,1,2{3,5,3}, Template:CDD, has truncated icosidodecahedron, truncated dodecahedron, and triangular prism cells, with a mirrored sphenoid vertex figure.

Runcinated icosahedral honeycomb

Runcinated icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t0,3{3,5,3}
Coxeter diagram	Template:CDD
Cells	{3,5} {}×{3}
Faces	triangle {3} square {4}
Vertex figure	pentagonal antiprism
Coxeter group	$2\times {\bar{J}}_3$, [[3,5,3]]
Properties	Vertex-transitive, edge-transitive

The runcinated icosahedral honeycomb, t_0,3{3,5,3}, Template:CDD, has icosahedron and triangular prism cells, with a pentagonal antiprism vertex figure.

Viewed from center of triangular prism

Runcitruncated icosahedral honeycomb

Runcitruncated icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t0,1,3{3,5,3}
Coxeter diagram	Template:CDD
Cells	t{3,5} rr{3,5} {}×{3} {}×{6}
Faces	triangle {3} square {4} pentagon {5} hexagon {6}
Vertex figure	isosceles-trapezoidal pyramid
Coxeter group	${\bar{J}}_3$, [3,5,3]
Properties	Vertex-transitive

The runcitruncated icosahedral honeycomb, t_0,1,3{3,5,3}, Template:CDD, has truncated icosahedron, rhombicosidodecahedron, hexagonal prism, and triangular prism cells, with an isosceles-trapezoidal pyramid vertex figure.

The runcicantellated icosahedral honeycomb is equivalent to the runcitruncated icosahedral honeycomb.

Viewed from center of triangular prism

Omnitruncated icosahedral honeycomb

Omnitruncated icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	t0,1,2,3{3,5,3}
Coxeter diagram	Template:CDD
Cells	tr{3,5} {}×{6}
Faces	square {4} hexagon {6} dodecagon {10}
Vertex figure	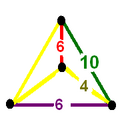phyllic disphenoid
Coxeter group	$2\times {\bar{J}}_3$, [[3,5,3]]
Properties	Vertex-transitive

The omnitruncated icosahedral honeycomb, t_0,1,2,3{3,5,3}, Template:CDD, has truncated icosidodecahedron and hexagonal prism cells, with a phyllic disphenoid vertex figure.

Centered on hexagonal prism

Omnisnub icosahedral honeycomb

Omnisnub icosahedral honeycomb
Type	Uniform honeycombs in hyperbolic space
Schläfli symbol	h(t0,1,2,3{3,5,3})
Coxeter diagram	Template:CDD
Cells	sr{3,5} s{2,3} irr. {3,3}
Faces	triangle {3} pentagon {5}
Vertex figure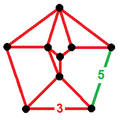
Coxeter group	[[3,5,3]]+
Properties	Vertex-transitive

The omnisnub icosahedral honeycomb, h(t_0,1,2,3{3,5,3}), Template:CDD, has snub dodecahedron, octahedron, and tetrahedron cells, with an irregular vertex figure. It is vertex-transitive, but cannot be made with uniform cells. Template:Clear

Partially diminished icosahedral honeycomb

Partially diminished icosahedral honeycomb Parabidiminished icosahedral honeycomb
Type	Uniform honeycombs
Schläfli symbol	pd{3,5,3}
Coxeter diagram	-
Cells	{5,3} s{2,5}
Faces	triangle {3} pentagon {5}
Vertex figure	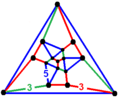tetrahedrally diminished dodecahedron
Coxeter group	1/5[3,5,3]+
Properties	Vertex-transitive

The partially diminished icosahedral honeycomb or parabidiminished icosahedral honeycomb, pd{3,5,3}, is a non-Wythoffian uniform honeycomb with dodecahedron and pentagonal antiprism cells, with a tetrahedrally diminished dodecahedron vertex figure. The icosahedral cells of the {3,5,3} are diminished at opposite vertices (parabidiminished), leaving a pentagonal antiprism (parabidiminished icosahedron) core, and creating new dodecahedron cells above and below.

Template:Clear

See also

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space
• Seifert–Weber space
• 11-cell - An abstract regular polychoron which shares the {3,5,3} Schläfli symbol.

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. Template:ISBN. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999 Template:ISBN (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables II, III, IV, V, p212-213)
• Norman Johnson Uniform Polytopes, Manuscript
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • N.W. Johnson: Geometries and Transformations, (2018) Chapter 13: Hyperbolic Coxeter groups
• Template:KlitzingPolytopes