Alternated hexagonal tiling honeycomb

Alternated hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb Semiregular honeycomb
Schläfli symbols	h{6,3,3} s{3,6,3} 2s{6,3,6} 2s{6,3[3]} s{3[3,3]}
Coxeter diagrams	Template:CDD ↔ Template:CDD Template:CDD Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD ↔ Template:CDD
Cells	{3,3} {3[3]}
Faces	triangle {3}
Vertex figure	Template:CDD truncated tetrahedron
Coxeter groups	${\bar{P}}_3$, [3,3[3]] 1/2 ${\bar{V}}_3$, [6,3,3] 1/2 ${\bar{Y}}_3$, [3,6,3] 1/2 ${\bar{Z}}_3$, [6,3,6] 1/2 ${\overline{VP}}_3$, [6,3[3]] 1/2 ${\overline{PP}}_3$, [3[3,3]]
Properties	Vertex-transitive, edge-transitive, quasiregular

In three-dimensional hyperbolic geometry, the alternated hexagonal tiling honeycomb, h{6,3,3}, Template:CDD or Template:CDD, is a semiregular tessellation with tetrahedron and triangular tiling cells arranged in an octahedron vertex figure. It is named after its construction, as an alteration of a hexagonal tiling honeycomb.

Symmetry constructions

Subgroup relations

It has five alternated constructions from reflectional Coxeter groups all with four mirrors and only the first being regular: Template:CDD [6,3,3], Template:CDD [3,6,3], Template:CDD [6,3,6], Template:CDD [6,3^[3]] and [3^[3,3]] Template:CDD, having 1, 4, 6, 12 and 24 times larger fundamental domains respectively. In Coxeter notation subgroup markups, they are related as: [6,(3,3)^*] (remove 3 mirrors, index 24 subgroup); [3,6,3^*] or [3^*,6,3] (remove 2 mirrors, index 6 subgroup); [1⁺,6,3,6,1⁺] (remove two orthogonal mirrors, index 4 subgroup); all of these are isomorphic to [3^[3,3]]. The ringed Coxeter diagrams are Template:CDD, Template:CDD, Template:CDD, Template:CDD and Template:CDD, representing different types (colors) of hexagonal tilings in the Wythoff construction. Template:-

Related honeycombs

The alternated hexagonal tiling honeycomb has 3 related forms: the cantic hexagonal tiling honeycomb, Template:CDD; the runcic hexagonal tiling honeycomb, Template:CDD; and the runcicantic hexagonal tiling honeycomb, Template:CDD.

Cantic hexagonal tiling honeycomb

Cantic hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	h2{6,3,3}
Coxeter diagrams	Template:CDD ↔ Template:CDD
Cells	r{3,3} t{3,3} h2{6,3}
Faces	triangle {3} hexagon {6}
Vertex figure	wedge
Coxeter groups	${\bar{P}}_3$, [3,3[3]]
Properties	Vertex-transitive

The cantic hexagonal tiling honeycomb, h₂{6,3,3}, Template:CDD or Template:CDD, is composed of octahedron, truncated tetrahedron, and trihexagonal tiling facets, with a wedge vertex figure.

Runcic hexagonal tiling honeycomb

Runcic hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	h3{6,3,3}
Coxeter diagrams	Template:CDD ↔ Template:CDD
Cells	{3,3} {}x{3} rr{3,3} {3[3]}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	triangular cupola
Coxeter groups	${\bar{P}}_3$, [3,3[3]]
Properties	Vertex-transitive

The runcic hexagonal tiling honeycomb, h₃{6,3,3}, Template:CDD or Template:CDD, has tetrahedron, triangular prism, cuboctahedron, and triangular tiling facets, with a triangular cupola vertex figure. Template:-

Runcicantic hexagonal tiling honeycomb

Runcicantic hexagonal tiling honeycomb
Type	Paracompact uniform honeycomb
Schläfli symbols	h2,3{6,3,3}
Coxeter diagrams	Template:CDD ↔ Template:CDD
Cells	t{3,3} {}x{3} tr{3,3} h2{6,3}
Faces	triangle {3} square {4} hexagon {6}
Vertex figure	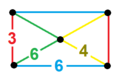rectangular pyramid
Coxeter groups	${\bar{P}}_3$, [3,3[3]]
Properties	Vertex-transitive

The runcicantic hexagonal tiling honeycomb, h_2,3{6,3,3}, Template:CDD or Template:CDD, has truncated tetrahedron, triangular prism, truncated octahedron, and trihexagonal tiling facets, with a rectangular pyramid vertex figure.

See also

• Convex uniform honeycombs in hyperbolic space
• Regular tessellations of hyperbolic 3-space
• Paracompact uniform honeycombs
• Semiregular honeycomb
• Hexagonal tiling honeycomb

References

• Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. Template:ISBN. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
• The Beauty of Geometry: Twelve Essays (1999), Dover Publications, Template:LCCN, Template:ISBN (Chapter 10, Regular Honeycombs in Hyperbolic Space Template:Webarchive) Table III
• Jeffrey R. Weeks The Shape of Space, 2nd edition Template:ISBN (Chapters 16–17: Geometries on Three-manifolds I,II)
• N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups (1999), Volume 4, Issue 4, pp 329–353 [1] [2]
• N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, Commensurability classes of hyperbolic Coxeter groups, (2002) H³: p130. [3]