12 equal temperament

12 equal temperament (12-ET)Template:Efn is the musical system that divides the octave into 12 parts, all of which are equally tempered (equally spaced) on a logarithmic scale, with a ratio equal to the 12th root of 2 ( ≈ 1.05946). That resulting smallest interval, Template:Frac the width of an octave, is called a semitone or half step.
Twelve-tone equal temperament is the most widespread system in music today. It has been the predominant tuning system of Western music, starting with classical music, since the 18th century, and Europe almost exclusively used approximations of it for millennia before that.Template:Citation needed It has also been used in other cultures.
In modern times, 12-ET is usually tuned relative to a standard pitch of 440 Hz, called A440, meaning one note, A4 (the A in the 4th octave of a typical 88-key piano), is tuned to 440 hertz and all other notes are defined as some multiple of semitones apart from it, either higher or lower in frequency. The standard pitch has not always been 440 Hz. It has varied and generally risen over the past few hundred years.Template:Sfn
History
The two figures frequently credited with the achievement of exact calculation of twelve-tone equal temperament are Zhu Zaiyu (also romanized as Chu-Tsaiyu. Chinese: Template:Lang) in 1584 and Simon Stevin in 1585. According to Fritz A. Kuttner, a critic of the theory,Template:Sfn it is known that "Chu-Tsaiyu presented a highly precise, simple and ingenious method for arithmetic calculation of equal temperament mono-chords in 1584" and that "Simon Stevin offered a mathematical definition of equal temperament plus a somewhat less precise computation of the corresponding numerical values in 1585 or later." The developments occurred independently.Template:Sfn
Kenneth Robinson attributes the invention of equal temperament to Zhu ZaiyuTemplate:Sfn and provides textual quotations as evidence.Template:Sfn Zhu Zaiyu is quoted as saying that, in a text dating from 1584, "I have founded a new system. I establish one foot as the number from which the others are to be extracted, and using proportions I extract them. Altogether one has to find the exact figures for the pitch-pipers in twelve operations."Template:Sfn Kuttner disagrees and remarks that his claim "cannot be considered correct without major qualifications."Template:Sfn Kuttner proposes that neither Zhu Zaiyu or Simon Stevin achieved equal temperament and that neither of the two should be treated as inventors.Template:Sfn
China
Early history
A complete set of bronze chime bells, among many musical instruments found in the tomb of the Marquis Yi of Zeng (early Warring States, Template:Circa in the Chinese Bronze Age), covers five full 7-note octaves in the key of C Major, including 12 note semi-tones in the middle of the range.Template:Sfn
An approximation for equal temperament was described by Template:Ill, a mathematician of the Southern and Northern Dynasties who lived from 370 to 447.[1] He came out with the earliest recorded approximate numerical sequence in relation to equal temperament in history: 900 849 802 758 715 677 638 601 570 536 509.5 479 450.Template:Sfn
Zhu Zaiyu

Zhu Zaiyu (Template:Lang), a prince of the Ming court, spent thirty years on research based on the equal temperament idea originally postulated by his father. He described his new pitch theory in his Fusion of Music and Calendar Template:Lang published in 1580. This was followed by the publication of a detailed account of the new theory of the equal temperament with a precise numerical specification for 12-ET in his 5,000-page work Complete Compendium of Music and Pitch (Yuelü quan shu Template:Lang) in 1584.Template:Sfn An extended account is also given by Joseph Needham.Template:Sfn Zhu obtained his result mathematically by dividing the length of string and pipe successively by Template:Radic ≈ 1.059463, and for pipe length by Template:Radic,Template:Sfn such that after twelve divisions (an octave) the length was divided by a factor of 2:
Similarly, after 84 divisions (7 octaves) the length was divided by a factor of 128:
Zhu Zaiyu has been credited as the first person to solve the equal temperament problem mathematically.Template:Sfn At least one researcher has proposed that Matteo Ricci, a Jesuit in China recorded this work in his personal journalTemplate:SfnTemplate:Sfn and may have transmitted the work back to Europe. (Standard resources on the topic make no mention of any such transfer.Template:Sfn) In 1620, Zhu's work was referenced by a European mathematician.Template:WhoTemplate:Sfn Murray Barbour said, "The first known appearance in print of the correct figures for equal temperament was in China, where Prince Tsaiyü's brilliant solution remains an enigma."Template:Sfn The 19th-century German physicist Hermann von Helmholtz wrote in On the Sensations of Tone that a Chinese prince (see below) introduced a scale of seven notes, and that the division of the octave into twelve semitones was discovered in China.Template:Sfn

Zhu Zaiyu illustrated his equal temperament theory by the construction of a set of 36 bamboo tuning pipes ranging in 3 octaves, with instructions of the type of bamboo, color of paint, and detailed specification on their length and inner and outer diameters. He also constructed a 12-string tuning instrument, with a set of tuning pitch pipes hidden inside its bottom cavity. In 1890, Victor-Charles Mahillon, curator of the Conservatoire museum in Brussels, duplicated a set of pitch pipes according to Zhu Zaiyu's specification. He said that the Chinese theory of tones knew more about the length of pitch pipes than its Western counterpart, and that the set of pipes duplicated according to the Zaiyu data proved the accuracy of this theory.
Europe

Early history
One of the earliest discussions of equal temperament occurs in the writing of Aristoxenus in the 4th century BC.Template:Sfn
Vincenzo Galilei (father of Galileo Galilei) was one of the first practical advocates of twelve-tone equal temperament. He composed a set of dance suites on each of the 12 notes of the chromatic scale in all the "transposition keys", and published also, in his 1584 "Fronimo", 24 + 1 ricercars.Template:Sfn He used the 18:17 ratio for fretting the lute (although some adjustment was necessary for pure octaves).Template:Sfn
Galilei's countryman and fellow lutenist Giacomo Gorzanis had written music based on equal temperament by 1567.Template:Sfn Gorzanis was not the only lutenist to explore all modes or keys: Francesco Spinacino wrote a Template:Lang (Ricercar in all the Tones) as early as 1507.[2] In the 17th century lutenist-composer John Wilson wrote a set of 30 preludes including 24 in all the major/minor keys.Template:SfnTemplate:Sfn Henricus Grammateus drew a close approximation to equal temperament in 1518. The first tuning rules in equal temperament were given by Giovani Maria Lanfranco in his "Scintille de musica".[3] Zarlino in his polemic with Galilei initially opposed equal temperament but eventually conceded to it in relation to the lute in his Template:Lang in 1588.
Simon Stevin
The first mention of equal temperament related to the twelfth root of two in the West appeared in Simon Stevin's manuscript Template:Lang (c. 1605), published posthumously nearly three centuries later in 1884.Template:Sfn However, due to insufficient accuracy of his calculation, many of the chord length numbers he obtained were off by one or two units from the correct values.Template:Sfn As a result, the frequency ratios of Simon Stevin's chords has no unified ratio, but one ratio per tone, which is claimed by Gene Cho as incorrect.Template:Sfn
The following were Simon Stevin's chord length from Template:Lang:Template:Sfn
| Tone | Chord 10000 from Simon Stevin | Ratio | Corrected chord |
|---|---|---|---|
| semitone | 9438 | 1.0595465 | 9438.7 |
| whole tone | 8909 | 1.0593781 | |
| tone and a half | 8404 | 1.0600904 | 8409 |
| ditone | 7936 | 1.0594758 | 7937 |
| ditone and a half | 7491 | 1.0594046 | 7491.5 |
| tritone | 7071 | 1.0593975 | 7071.1 |
| tritone and a half | 6674 | 1.0594845 | 6674.2 |
| four-tone | 6298 | 1.0597014 | 6299 |
| four-tone and a half | 5944 | 1.0595558 | 5946 |
| five-tone | 5611 | 1.0593477 | 5612.3 |
| five-tone and a half | 5296 | 1.0594788 | 5297.2 |
| full tone | 1.0592000 |
A generation later, French mathematician Marin Mersenne presented several equal tempered chord lengths obtained by Jean Beaugrand, Ismael Bouillaud, and Jean Galle.Template:Sfn
In 1630 Johann Faulhaber published a 100-cent monochord table, which contained several errors due to his use of logarithmic tables. He did not explain how he obtained his results.Template:Sfn
Baroque era
From 1450 to about 1800, plucked instrument players (lutenists and guitarists) generally favored equal temperament,[4] and the Brossard lute manuscript compiled in the last quarter of the 17th century contains a series of 18 preludes attributed to Bocquet written in all keys, including the last prelude, entitled Template:Lang, which enharmonically modulates through all keys.[5]Template:Huh? Angelo Michele Bartolotti published a series of passacaglias in all keys, with connecting enharmonically modulating passages. Among the 17th-century keyboard composers Girolamo Frescobaldi advocated equal temperament. Some theorists, such as Giuseppe Tartini, were opposed to the adoption of equal temperament; they felt that degrading the purity of each chord degraded the aesthetic appeal of music, although Andreas Werckmeister emphatically advocated equal temperament in his 1707 treatise published posthumously.[6]
Twelve-tone equal temperament took hold for a variety of reasons. It was a convenient fit for the existing keyboard design, and permitted total harmonic freedom with the burden of moderate impurity in every interval, particularly imperfect consonances. This allowed greater expression through enharmonic modulation, which became extremely important in the 18th century in music of such composers as Francesco Geminiani, Wilhelm Friedemann Bach, Carl Philipp Emmanuel Bach, and Johann Gottfried Müthel.Template:Citation needed Twelve-tone equal temperament did have some disadvantages, such as imperfect thirds, but as Europe switched to equal temperament, it changed the music that it wrote in order to accommodate the system and minimize dissonance.Template:Efn
The progress of equal temperament from the mid-18th century on is described with detail in quite a few modern scholarly publications: It was already the temperament of choice during the Classical era (second half of the 18th century),Template:Citation needed and it became standard during the Early Romantic era (first decade of the 19th century),Template:Citation needed except for organs that switched to it more gradually, completing only in the second decade of the 19th century. (In England, some cathedral organists and choirmasters held out against it even after that date; Samuel Sebastian Wesley, for instance, opposed it all along. He died in 1876.)Template:Citation needed
A precise equal temperament is possible using the 17th century Sabbatini method of splitting the octave first into three tempered major thirds.Template:Sfn This was also proposed by several writers during the Classical era. Tuning without beat rates but employing several checks, achieving virtually modern accuracy, was already done in the first decades of the 19th century.Template:Sfn Using beat rates, first proposed in 1749, became common after their diffusion by Helmholtz and Ellis in the second half of the 19th century.Template:Sfn The ultimate precision was available with 2 decimal tables published by White in 1917.[7]
It is in the environment of equal temperament that the new styles of symmetrical tonality and polytonality, atonal music such as that written with the twelve tone technique or serialism, and jazz (at least its piano component) developed and flourished.
Comparison of historical approximations of the semitone
| Year | Name | RatioTemplate:Sfn | Cents |
|---|---|---|---|
| 400 | He Chengtian | 1.060070671 | 101.0 |
| 1580 | Vincenzo Galilei | 18:17 [1.058823529] | 99.0 |
| 1581 | Zhu Zaiyu | 1.059463094 | 100.0 |
| 1585 | Simon Stevin | 1.059546514 | 100.1 |
| 1630 | Marin Mersenne | 1.059322034 | 99.8 |
| 1630 | Johann Faulhaber | 1.059490385 | 100.0 |
Mathematical properties

In twelve-tone equal temperament, which divides the octave into 12 equal parts, the width of a semitone, i.e. the frequency ratio of the interval between two adjacent notes, is the twelfth root of two:
This interval is divided into 100 cents.
Calculating absolute frequencies
Template:See also To find the frequency, Template:Math, of a note in 12-ET, the following definition may be used:
In this formula Template:Math refers to the pitch, or frequency (usually in hertz), you are trying to find. Template:Math refers to the frequency of a reference pitch. Template:Mvar and Template:Mvar refer to numbers assigned to the desired pitch and the reference pitch, respectively. These two numbers are from a list of consecutive integers assigned to consecutive semitones. For example, A4 (the reference pitch) is the 49th key from the left end of a piano (tuned to 440 Hz), and C4 (middle C), and F#4 are the 40th and 46th key respectively. These numbers can be used to find the frequency of C4 and F#4:
Just intervals
The intervals of 12-ET closely approximate some intervals in just intonation.Template:Sfn
By limit
12 ET is very accurate in the 3 limit, but as one increases prime limits to 11, it gradually gets worse by about a sixth of a semitone each time. Its eleventh and thirteenth harmonics are extremely inaccurate. 12 ET's seventeenth and nineteenth harmonics are almost as accurate as its third harmonic, but by this point, the prime limit has gotten too high to sound consonant to most people.Template:Citation needed
3 limit
Template:See also 12 ET has a very good approximation of the perfect fifth Template:Nobr and its inversion, the perfect fourth Template:Nobr especially for the division of the octave into a relatively small number of tones. Specifically, a just perfect fifth is only one fifty-first of a semitone sharper than the equally-tempered approximation. Because the major tone Template:Nobr is simply two perfect fifths minus an octave, and its inversion, the Pythagorean minor seventh Template:Nobr is simply two perfect fourths combined, they, for the most part, retain the accuracy of their predecessors; the error is doubled, but it remains small – so small, in fact, that humans cannot perceive it. One can continue to use fractions with higher powers of three, the next two being Template:Sfrac and Template:Sfrac, but as the terms of the fractions grow larger, they become less pleasing to the ear.Template:Citation needed
5 limit
Template:See also 12 ET's approximation of the fifth harmonic (Template:Sfrac) is approximately one-seventh of a semitone off. Because intervals that are less than a quarter of a scale step off still sound in tune, other five-limit intervals in 12 ET, such as Template:Sfrac and Template:Sfrac, have similarly sized errors. The major triad, therefore, sounds in tune as its frequency ratio is approximately 4:5:6, further, merged with its first inversion, and two sub-octave tonics, it is 1:2:3:4:5:6, all six lowest natural harmonics of the bass tone.Template:Citation needed
7 limit
Template:See also 12 ET's approximation of the seventh harmonic (Template:Sfrac) is about one-third of a semitone off. Because the error is greater than a quarter of a semitone, seven-limit intervals in 12 ET tend to sound out of tune. In the tritone fractions Template:Sfrac and Template:Sfrac, the errors of the fifth and seventh harmonics partially cancel each other out so that the just fractions are within a quarter of a semitone of their equally-tempered equivalents.Template:Citation needed
11 and 13 limits
The eleventh harmonic (Template:Sfrac), at 551.32 cents, falls almost exactly halfway between the nearest two equally-tempered intervals in 12 ET and therefore is not approximated by either. In fact, Template:Sfrac is almost as far from any equally-tempered approximation as possible in 12 ET. The thirteenth harmonic (Template:Sfrac), at two-fifths of a semitone sharper than a minor sixth, is almost as inaccurate. Although this means that the fraction Template:Sfrac and also its inversion (Template:Sfrac) are accurately approximated (specifically, by three semitones), since the errors of the eleventh and thirteenth harmonics mostly cancel out, most people who are not familiar with quarter tones or microtonality will not be familiar with the eleventh and thirteenth harmonics. Similarly, while the error of the eleventh or thirteenth harmonic could be mostly canceled out by the error of the seventh harmonic, most Western musicians would not find the resulting fractions consonant since 12 ET does not approximate them accurately.Template:Citation needed
17 and 19 limits
The seventeenth harmonic (Template:Sfrac) is only about 5 cents sharper than one semitone in 12 ET. It can be combined with 12 ET's approximation of the third harmonic in order to yield Template:Sfrac, which is, as the next Pell approximation after Template:Sfrac, only about three cents away from the equally-tempered tritone (the square root of two), and Template:Sfrac, which is only one cent away from 12 ET's major seventh. The nineteenth harmonic is only about 2.5 cents flatter than three of 12 ET's semitones, so it can likewise be combined with the third harmonic to yield Template:Sfrac, which is about 4.5 cents flatter than an equally-tempered minor sixth, and Template:Sfrac, which is about 6.5 cents flatter than a semitone. However, because 17 and 19 are rather large for consonant ratios and most people are unfamiliar with 17 limit and 19 limit intervals, 17 limit and 19 limit intervals are not useful for most purposes, so they can likely not be judged as playing a part in any consonances of 12 ET.Template:Citation needed
Table
In the following table the sizes of various just intervals are compared against their equal-tempered counterparts, given as a ratio as well as cents. Differences of less than six cents cannot be noticed by most people, and intervals that are more than a quarter of a step; which in this case is 25 cents, off sound out of tune.Template:Citation needed
Commas
12-ET tempers out several commas, meaning that there are several fractions close to Template:Sfrac that are treated as Template:Sfrac by 12-ET due to its mapping of different fractions to the same equally-tempered interval. For example, Template:Sfrac (Template:Sfrac) and Template:Sfrac (Template:Sfrac) are each mapped to the tritone, so they are treated as nominally the same interval; therefore, their quotient, Template:Sfrac (Template:Sfrac) is mapped to/treated as unison. This is the Pythagorean comma, and it is 12-ET's only 3-limit comma. However, as one increases the prime limit and includes more intervals, the number of commas increases. 12-ET's most important five-limit comma is Template:Sfrac (Template:Sfrac), which is known as the syntonic comma and is the factor between Pythagorean thirds and sixths and their just counterparts. 12-ET's other 5-limit commas include:
- Schisma: Template:Sfrac = Template:Sfrac = (Template:Sfrac)1 × (Template:Sfrac)−1
- Diaschisma: Template:Sfrac = Template:Sfrac = (Template:Sfrac)−1 × (Template:Sfrac)2
- Lesser diesis: Template:Sfrac = Template:Sfrac = (Template:Sfrac)−1 × (Template:Sfrac)3
- Greater diesis: Template:Sfrac = Template:Sfrac=(Template:Sfrac)−1 × (Template:Sfrac)4
One of the 7-limit commas that 12-ET tempers out is the septimal kleisma, which is equal to Template:Sfrac, or Template:Nowrap 12-ET's other 7-limit commas include:
- Septimal semicomma: Template:Sfrac = Template:Sfrac = (Template:Sfrac)1 × (Template:Sfrac)−1
- Archytas' comma: Template:Sfrac = Template:Sfrac = Template:Nowrap
- Septimal quarter tone: Template:Sfrac = Template:Sfrac = (Template:Sfrac)−1 × (Template:Sfrac)3 × (Template:Sfrac)1
- Jubilisma: Template:Sfrac = Template:Sfrac = (Template:Sfrac)−1 × (Template:Sfrac)2 × Template:Nowrap
Scale diagram
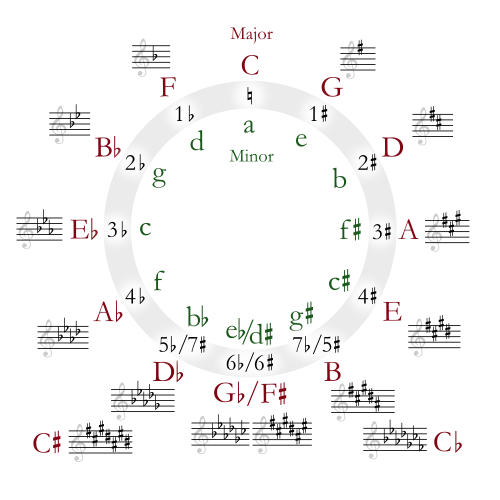
Modes
Ionian mode (major scale)
Dorian mode
Phrygian mode
Lydian mode
Mixolydian mode
Aeolian mode (natural minor scale)
Locrian mode
See also
- Archicembalo, instrument with a double keyboard layout consisting of a 19 tone system close to 19tet in pitch with an additional 12 tone keyboard that is tuned approximately a quartertone in between the white keys of the 19 tone keyboard.
- Beta scale
- Elaine Walker (composer)
- Meantone temperament
- Musical temperament
- 23 tone equal temperament
- 31 tone equal temperament
Similar tuning systems
Historically, multiple tuning systems have been used that can be seen as slight variations of 12-TEDO, with twelve notes per octave but with some variation among interval sizes so that the notes are not quite equally-spaced. One example of this a three-limit scale where equally-tempered perfect fifths of 700 cents are replaced with justly-intoned perfect fifths of 701.955 cents. Because the two intervals differ by less than 2 cents, or Template:Frac of an octave, the two scales are very similar. In fact, the Chinese developed 3-limit just intonation at least a century before He Chengtian created the sequence of 12-TEDO.Template:Sfn Likewise, Pythagorean tuning, which was developed by ancient Greeks, was the predominant system in Europe until during the Renaissance, when Europeans realized that dissonant intervals such as Template:FracTemplate:Sfn could be made more consonant by tempering them to simpler ratios like Template:Frac, resulting in Europe developing a series of meantone temperaments that slightly modified the interval sizes but could still be viewed as an approximate of 12-TEDO. Due to meantone temperaments' tendency to concentrate error onto one enharmonic perfect fifth, making it very dissonant, European music theorists, such as Andreas Werckmeister, Johann Philipp Kirnberger, Francesco Antonio Vallotti, and Thomas Young, created various well temperaments with the goal of dividing up the commas in order to reduce the dissonance of the worst-affected intervals. Werckmeister and Kirnberger were each dissatisfied with his first temperament and therefore created multiple temperaments, the latter temperaments more closely approximating equal temperament than the former temperaments. Likewise, Europe as a whole gradually transitioned from meantone and well temperaments to 12-TEDO, the system that it still uses today.
Subsets
Template:See also While some types of music, such as serialism, use all twelve notes of 12-TEDO, most music only uses notes from a particular subset of 12-TEDO known as a scale. Many different types of scales exist.
The most popular type of scale in 12-TEDO is meantone. Meantone refers to any scale where all of its notes are consecutive on the circle of fifths. Meantone scales of different sizes exist, and some meantone scales used include five-note meantone, seven-note meantone, and nine-note meantone. Meantone is present in the design of Western instruments. For example, the keys of a piano and its predecessors are structured so that the white keys form a seven-note meantone scale and the black keys form a five-note meantone scale. Another example is that guitars and other string instruments with at least five strings are typically tuned so that their open strings form a five-note meantone scale.
Other scales used in 12-TEDO include the ascending melodic minor scale, the harmonic minor, the harmonic major, the diminished scale, and the in scale.
See also
- Equal temperament
- Just intonation
- Musical acoustics (the physics of music)
- Music and mathematics
- Microtonal music
- List of meantone intervals
- Diatonic and chromatic
- Electronic tuner
- Musical tuning
References
Footnotes
Citations
Sources
- Template:Cite book
- Template:Cite book
- Template:Cite book
- Template:Cite journal
- Template:Cite book
- Template:Cite journal
- Template:Cite book
- Template:Cite book
- Template:Cite book
- Template:Citation
- Template:Cite book
- Template:Cite journal
- Template:Cite book
- Template:Cite web
- Template:Cite journal
- Template:Cite book
- Template:Cite book
- Template:Cite book
- Template:Cite book
- Template:Cite book
- Template:Cite journal
- Template:Cite book
- Template:Cite web
Further reading
- Duffin, Ross W. How Equal Temperament Ruined Harmony (and Why You Should Care). W.W. Norton & Company, 2007.
- Jorgensen, Owen. Tuning. Michigan State University Press, 1991. Template:ISBN
- Khramov, Mykhaylo. "Approximation of 5-limit just intonation. Computer MIDI Modeling in Negative Systems of Equal Divisions of the Octave", Proceedings of the International Conference SIGMAP-2008Template:Dead link, 26–29 July 2008, Porto, pp. 181–184, Template:ISBN
- Surjodiningrat, W., Sudarjana, P.J., and Susanto, A. (1972) Tone measurements of outstanding Javanese gamelans in Jogjakarta and Surakarta, Gadjah Mada University Press, Jogjakarta 1972. Cited on https://web.archive.org/web/20050127000731/http://web.telia.com/~u57011259/pelog_main.htm. Retrieved May 19, 2006.
- Stewart, P. J. (2006) "From Galaxy to Galaxy: Music of the Spheres" [1]
- Sensations of Tone a foundational work on acoustics and the perception of sound by Hermann von Helmholtz. Especially Appendix XX: Additions by the Translator, pages 430–556, (pdf pages 451–577)]
External links
- Xenharmonic wiki on EDOs vs. Equal Temperaments
- Huygens-Fokker Foundation Centre for Microtonal Music
- A.Orlandini: Music Acoustics
- "Temperament" from A supplement to Mr. Chambers's cyclopædia (1753)
- Barbieri, Patrizio. Enharmonic instruments and music, 1470–1900 Template:Webarchive. (2008) Latina, Il Levante Libreria Editrice
- Fractal Microtonal Music, Jim Kukula.
- All existing 18th century quotes on J.S. Bach and temperament
- Dominic Eckersley: "Rosetta Revisited: Bach's Very Ordinary Temperament"
- Well Temperaments, based on the Werckmeister Definition
- FAVORED CARDINALITIES OF SCALES by PETER BUCH
- ↑ Template:Cite journal
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedappstate.edu - ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedScintille - ↑ Lindley, Mark. Lutes, Viols, Temperaments. Template:ISBN
- ↑ Vm7 6214
- ↑ Andreas Werckmeister (1707), Template:Lang
- ↑ Template:Cite book