Small snub icosicosidodecahedron

Template:Short description Template:Uniform polyhedra db File:Small snub icosicosidododecahedron.stl

In geometry, the small snub icosicosidodecahedron or snub disicosidodecahedron is a uniform star polyhedron, indexed as U₃₂. It has 112 faces (100 triangles and 12 pentagrams), 180 edges, and 60 vertices. Its stellation core is a truncated pentakis dodecahedron. It also called a holosnub icosahedron, Template:Math

The 40 non-snub triangular faces form 20 coplanar pairs, forming star hexagons that are not quite regular. Unlike most snub polyhedra, it has reflection symmetries.

Convex hull

Its convex hull is a nonuniform truncated icosahedron.

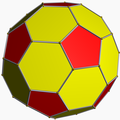Truncated icosahedron (regular faces)

Convex hull (isogonal hexagons)

Small snub icosicosidodecahedron

Cartesian coordinates

Let $\xi =-\frac{3}{2}+\frac{1}{2}\sqrt{1+4\varphi }\approx -0.1332396008261379$ be largest (least negative) zero of the polynomial $P=x^2+3x+{\varphi }^{-2}$, where $\varphi$ is the golden ratio. Let the point $p$ be given by

$p=\left(\begin{array}{c}{\varphi }^{-1}\xi +{\varphi }^{-3}\\ \xi \\ {\varphi }^{-2}\xi +{\varphi }^{-2}\end{array}\right)$.

Let the matrix $M$ be given by

$M=\left(\begin{array}{ccc}1/2& -\varphi /2& 1/(2\varphi )\\ \varphi /2& 1/(2\varphi )& -1/2\\ 1/(2\varphi )& 1/2& \varphi /2\end{array}\right)$.

$M$ is the rotation around the axis $(1,0,\varphi )$ by an angle of $2\pi /5$, counterclockwise. Let the linear transformations $T_0,\dots ,T_{11}$ be the transformations which send a point $(x,y,z)$ to the even permutations of $(\pm x,\pm y,\pm z)$ with an even number of minus signs. The transformations $T_i$ constitute the group of rotational symmetries of a regular tetrahedron. The transformations $T_i{M}^j$ $(i=0,\dots ,11$, $j=0,\dots ,4)$ constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points $T_i{M}^{j}p$ are the vertices of a small snub icosicosidodecahedron. The edge length equals $-2\xi$, the circumradius equals $\sqrt{-4\xi -{\varphi }^{-2}}$, and the midradius equals $\sqrt{-\xi }$.

For a small snub icosicosidodecahedron whose edge length is 1, the circumradius is

$R=\frac{1}{2}\sqrt{\frac{\xi -1}{\xi }}\approx 1.4581903307387025$

Its midradius is

$r=\frac{1}{2}\sqrt{\frac{-1}{\xi }}\approx 1.369787954633799$

The other zero of $P$ plays a similar role in the description of the small retrosnub icosicosidodecahedron.

See also

• List of uniform polyhedra
• Small retrosnub icosicosidodecahedron

External links

• Template:Mathworld
• Template:KlitzingPolytopes

Template:Polyhedron-stub