Power iteration

Template:Short description Template:Use dmy dates In mathematics, power iteration (also known as the power method) is an eigenvalue algorithm: given a diagonalizable matrix $A$, the algorithm will produce a number $\lambda$, which is the greatest (in absolute value) eigenvalue of $A$, and a nonzero vector $v$, which is a corresponding eigenvector of $\lambda$, that is, $Av=\lambda v$. The algorithm is also known as the Von Mises iteration.

Power iteration is a very simple algorithm, but it may converge slowly. The most time-consuming operation of the algorithm is the multiplication of matrix $A$ by a vector, so it is effective for a very large sparse matrix with appropriate implementation. The speed of convergence is like $({\lambda }_1/{\lambda }_2{)}^k$(see a later section). In words, convergence is exponential with base being the spectral gap.

The method

File:Animation of the Power Iteration Algorithm.gif

Animation that visualizes the power iteration algorithm on a 2x2 matrix. The matrix is depicted by its two eigenvectors. Error is computed as $||\text{approximation}-\text{largest eigenvector}||$

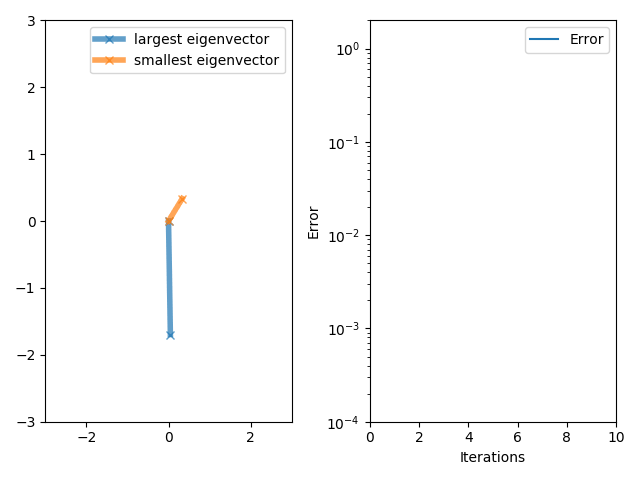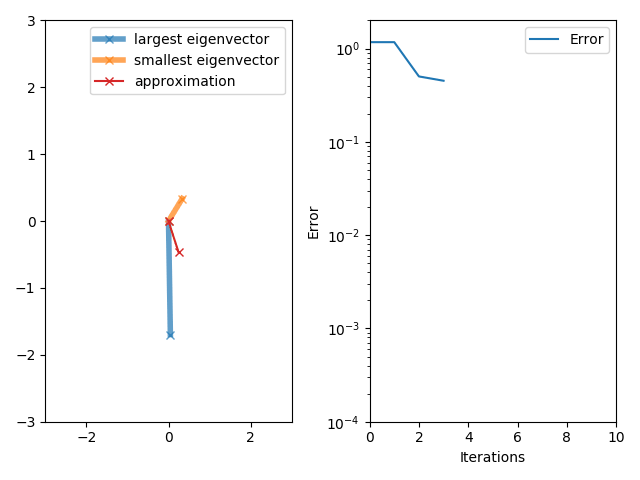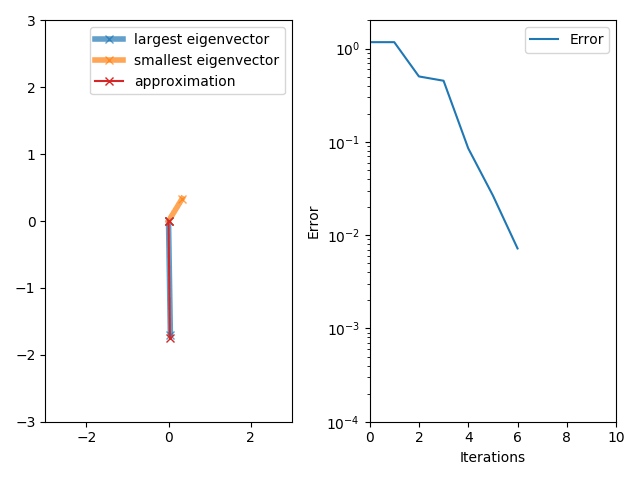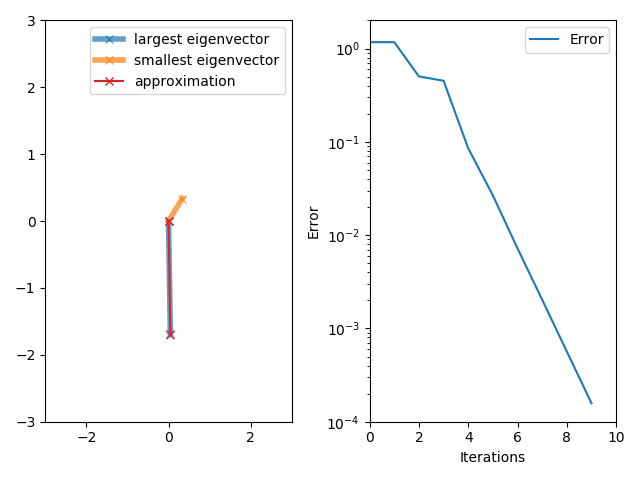
The power iteration algorithm starts with a vector $b_0$, which may be an approximation to the dominant eigenvector or a random vector. The method is described by the recurrence relation

$b_{k+1}=\frac{A{b}_k}{\Vert A{b}_k\Vert }$

So, at every iteration, the vector $b_k$ is multiplied by the matrix $A$ and normalized.

If we assume $A$ has an eigenvalue that is strictly greater in magnitude than its other eigenvalues and the starting vector $b_0$ has a nonzero component in the direction of an eigenvector associated with the dominant eigenvalue, then a subsequence $\left(b_k\right)$ converges to an eigenvector associated with the dominant eigenvalue.

Without the two assumptions above, the sequence $\left(b_k\right)$ does not necessarily converge. In this sequence,

$b_k=e^{i{\varphi }_k}{v}_1+r_k$,

where $v_1$ is an eigenvector associated with the dominant eigenvalue, and $\Vert r_k\Vert \to 0$. The presence of the term $e^{i{\varphi }_k}$ implies that $\left(b_k\right)$ does not converge unless $e^{i{\varphi }_k}=1$. Under the two assumptions listed above, the sequence $\left({\mu }_k\right)$ defined by

${\mu }_k=\frac{b_k^{*}A{b}_k}{b_k^{*}{b}_k}$

converges to the dominant eigenvalue (with Rayleigh quotient).Template:Clarify

One may compute this with the following algorithm (shown in Python with NumPy):

#!/usr/bin/env python3

import numpy as np

def power_iteration(A, num_iterations: int):
    # Ideally choose a random vector
    # To decrease the chance that our vector
    # Is orthogonal to the eigenvector
    b_k = np.random.rand(A.shape[1])

    for _ in range(num_iterations):
        # calculate the matrix-by-vector product Ab
        b_k1 = np.dot(A, b_k)

        # calculate the norm
        b_k1_norm = np.linalg.norm(b_k1)

        # re normalize the vector
        b_k = b_k1 / b_k1_norm

    return b_k

power_iteration(np.array([[0.5, 0.5], [0.2, 0.8]]), 10)

The vector $b_k$ converges to an associated eigenvector. Ideally, one should use the Rayleigh quotient in order to get the associated eigenvalue.

This algorithm is used to calculate the Google PageRank.

The method can also be used to calculate the spectral radius (the eigenvalue with the largest magnitude, for a square matrix) by computing the Rayleigh quotient

$\rho (A)=\max \{|{\lambda }_1|,\dots ,|{\lambda }_n|\}=\frac{b_k^{\mathrm{\top }}A{b}_k}{b_k^{\mathrm{\top }}{b}_k}.$

Analysis

Let $A$ be decomposed into its Jordan canonical form: $A=VJ{V}^{-1}$, where the first column of $V$ is an eigenvector of $A$ corresponding to the dominant eigenvalue ${\lambda }_1$. Since generically, the dominant eigenvalue of $A$ is unique, the first Jordan block of $J$ is the $1\times 1$ matrix $[{\lambda }_1],$ where ${\lambda }_1$ is the largest eigenvalue of A in magnitude. The starting vector $b_0$ can be written as a linear combination of the columns of V:

$b_0=c_1{v}_1+c_2{v}_2+\cdots +c_n{v}_n.$

By assumption, $b_0$ has a nonzero component in the direction of the dominant eigenvalue, so $c_1\ne 0$.

The computationally useful recurrence relation for $b_{k+1}$ can be rewritten as:

$b_{k+1}=\frac{A{b}_k}{\Vert A{b}_k\Vert }=\frac{A^{k+1}{b}_0}{\Vert A^{k+1}{b}_0\Vert },$

where the expression: $\frac{A^{k+1}{b}_0}{\Vert A^{k+1}{b}_0\Vert }$ is more amenable to the following analysis.

$\begin{array}{cc}{b}_k& =\frac{A^k{b}_0}{\Vert A^k{b}_0\Vert }\\ & =\frac{{\left(VJ{V}^{-1}\right)}^k{b}_0}{\Vert {\left(VJ{V}^{-1}\right)}^k{b}_0\Vert }\\ & =\frac{V{J}^k{V}^{-1}{b}_0}{\Vert V{J}^k{V}^{-1}{b}_0\Vert }\\ & =\frac{V{J}^k{V}^{-1}(c_1{v}_1+c_2{v}_2+\cdots +c_n{v}_n)}{\Vert V{J}^k{V}^{-1}(c_1{v}_1+c_2{v}_2+\cdots +c_n{v}_n)\Vert }\\ & =\frac{V{J}^k(c_1{e}_1+c_2{e}_2+\cdots +c_n{e}_n)}{\Vert V{J}^k(c_1{e}_1+c_2{e}_2+\cdots +c_n{e}_n)\Vert }\\ & ={\left(\frac{{\lambda }_1}{|{\lambda }_1|}\right)}^k\frac{c_1}{|c_1|}\frac{v_1+\frac{1}{c_1}V{\left(\frac{1}{{\lambda }_1}J\right)}^k(c_2{e}_2+\cdots +c_n{e}_n)}{\Vert v_1+\frac{1}{c_1}V{\left(\frac{1}{{\lambda }_1}J\right)}^k(c_2{e}_2+\cdots +c_n{e}_n)\Vert }\end{array}$

The expression above simplifies as $k\to \mathrm{\infty }$

${\left(\frac{1}{{\lambda }_1}J\right)}^k=\left[\begin{array}{ccccc}[1]& & & & \\ & {\left(\frac{1}{{\lambda }_1}{J}_2\right)}^k& & & \\ & & \ddots & \\ & & & {\left(\frac{1}{{\lambda }_1}{J}_m\right)}^k\end{array}\right]\to \left[\begin{array}{ccccc}1& & & & \\ & 0& & & \\ & & \ddots & \\ & & & 0\end{array}\right]\text{as}k\to \mathrm{\infty }.$

The limit follows from the fact that the eigenvalue of $\frac{1}{{\lambda }_1}{J}_i$ is less than 1 in magnitude, so

${\left(\frac{1}{{\lambda }_1}{J}_i\right)}^k\to 0\text{as}k\to \mathrm{\infty }.$

It follows that:

$\frac{1}{c_1}V{\left(\frac{1}{{\lambda }_1}J\right)}^k(c_2{e}_2+\cdots +c_n{e}_n)\to 0\text{as}k\to \mathrm{\infty }$

Using this fact, $b_k$ can be written in a form that emphasizes its relationship with $v_1$ when k is large:

$\begin{array}{cc}{b}_k& ={\left(\frac{{\lambda }_1}{|{\lambda }_1|}\right)}^k\frac{c_1}{|c_1|}\frac{v_1+\frac{1}{c_1}V{\left(\frac{1}{{\lambda }_1}J\right)}^k(c_2{e}_2+\cdots +c_n{e}_n)}{\Vert v_1+\frac{1}{c_1}V{\left(\frac{1}{{\lambda }_1}J\right)}^k(c_2{e}_2+\cdots +c_n{e}_n)\Vert }\\ & =e^{i{\varphi }_k}\frac{c_1}{|c_1|}\frac{v_1}{\Vert v_1\Vert }+r_k\end{array}$

where $e^{i{\varphi }_k}={({\lambda }_1/|{\lambda }_1|)}^k$ and $\Vert r_k\Vert \to 0$ as $k\to \mathrm{\infty }$

The sequence $\left(b_k\right)$ is bounded, so it contains a convergent subsequence. Note that the eigenvector corresponding to the dominant eigenvalue is only unique up to a scalar, so although the sequence $\left(b_k\right)$ may not converge, $b_k$ is nearly an eigenvector of A for large k.

Alternatively, if A is diagonalizable, then the following proof yields the same result

Let λ₁, λ₂, ..., λ_m be the m eigenvalues (counted with multiplicity) of A and let v₁, v₂, ..., v_m be the corresponding eigenvectors. Suppose that ${\lambda }_1$ is the dominant eigenvalue, so that $|{\lambda }_1|>|{\lambda }_j|$ for $j>1$.

The initial vector $b_0$ can be written:

$b_0=c_1{v}_1+c_2{v}_2+\cdots +c_m{v}_m.$

If $b_0$ is chosen randomly (with uniform probability), then c₁ ≠ 0 with probability 1. Now,

$\begin{array}{cc}{A}^k{b}_0& =c_1{A}^k{v}_1+c_2{A}^k{v}_2+\cdots +c_m{A}^k{v}_m\\ & =c_1{\lambda }_1^k{v}_1+c_2{\lambda }_2^k{v}_2+\cdots +c_m{\lambda }_m^k{v}_m\\ & =c_1{\lambda }_1^k(v_1+\frac{c_2}{c_1}{\left(\frac{{\lambda }_2}{{\lambda }_1}\right)}^k{v}_2+\cdots +\frac{c_m}{c_1}{\left(\frac{{\lambda }_m}{{\lambda }_1}\right)}^k{v}_m)\\ & \to c_1{\lambda }_1^k{v}_1& & \left|\frac{{\lambda }_j}{{\lambda }_1}\right|<1\text{ for }j>1\end{array}$

On the other hand:

$b_k=\frac{A^k{b}_0}{\Vert A^k{b}_0\Vert }.$

Therefore, $b_k$ converges to (a multiple of) the eigenvector $v_1$. The convergence is geometric, with ratio

$\left|\frac{{\lambda }_2}{{\lambda }_1}\right|,$

where ${\lambda }_2$ denotes the second dominant eigenvalue. Thus, the method converges slowly if there is an eigenvalue close in magnitude to the dominant eigenvalue.

Applications

Although the power iteration method approximates only one eigenvalue of a matrix, it remains useful for certain computational problems. For instance, Google uses it to calculate the PageRank of documents in their search engine, and Twitter uses it to show users recommendations of whom to follow. The power iteration method is especially suitable for sparse matrices, such as the web matrix, or as the matrix-free method that does not require storing the coefficient matrix $A$ explicitly, but can instead access a function evaluating matrix-vector products $Ax$. For non-symmetric matrices that are well-conditioned the power iteration method can outperform more complex Arnoldi iteration. For symmetric matrices, the power iteration method is rarely used, since its convergence speed can be easily increased without sacrificing the small cost per iteration; see, e.g., Lanczos iteration and LOBPCG.

Some of the more advanced eigenvalue algorithms can be understood as variations of the power iteration. For instance, the inverse iteration method applies power iteration to the matrix $A^{-1}$. Other algorithms look at the whole subspace generated by the vectors $b_k$. This subspace is known as the Krylov subspace. It can be computed by Arnoldi iteration or Lanczos iteration. Gram iteration is a super-linear and deterministic method to compute the largest eigenpair.

See also

• Rayleigh quotient iteration
• Inverse iteration