List of aperiodic sets of tiles

Template:Show

In geometry, a tiling is a partition of the plane (or any other geometric setting) into closed sets (called tiles), without gaps or overlaps (other than the boundaries of the tiles). A tiling is considered periodic if there exist translations in two independent directions which map the tiling onto itself. Such a tiling is composed of a single fundamental unit or primitive cell which repeats endlessly and regularly in two independent directions. An example of such a tiling is shown in the adjacent diagram (see the image description for more information). A tiling that cannot be constructed from a single primitive cell is called nonperiodic. If a given set of tiles allows only nonperiodic tilings, then this set of tiles is called aperiodic. The tilings obtained from an aperiodic set of tiles are often called aperiodic tilings, though strictly speaking it is the tiles themselves that are aperiodic. (The tiling itself is said to be "nonperiodic".)

The first table explains the abbreviations used in the second table. The second table contains all known aperiodic sets of tiles and gives some additional basic information about each set. This list of tiles is still incomplete.

Explanations

Abbreviation	Meaning	Explanation
E2	Euclidean plane	normal flat plane
H2	hyperbolic plane	plane, where the parallel postulate does not hold
E3	Euclidean 3 space	space defined by three perpendicular coordinate axes
MLD	Mutually locally derivable	two tilings are said to be mutually locally derivable from each other, if one tiling can be obtained from the other by a simple local rule (such as deleting or inserting an edge)

List

Image	Name	Number of tiles	Space	Publication Date	Refs.	Comments
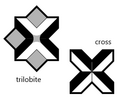	Trilobite and cross tiles	2	E2	1999		Tilings MLD from the chair tilings.
	Penrose P1 tiles	6	E2	1974		Tilings MLD from the tilings by P2 and P3, Robinson triangles, and "Starfish, ivy leaf, hex".
	Penrose P2 tiles	2	E2	1977		Tilings MLD from the tilings by P1 and P3, Robinson triangles, and "Starfish, ivy leaf, hex".
	Penrose P3 tiles	2	E2	1978		Tilings MLD from the tilings by P1 and P2, Robinson triangles, and "Starfish, ivy leaf, hex".
	Binary tiles	2	E2	1988		Although similar in shape to the P3 tiles, the tilings are not MLD from each other. Developed in an attempt to model the atomic arrangement in binary alloys.
	Robinson tiles	6	E2	1971		Tiles enforce aperiodicity by forming an infinite hierarchy of square lattices.
	Ammann A1 tiles	6	E2	1977		Tiles enforce aperiodicity by forming an infinite hierarchal binary tree.
	Ammann A2 tiles	2	E2	1986
	Ammann A3 tiles	3	E2	1986
	Ammann A4 tiles	2	E2	1986		Tilings MLD with Ammann A5.
	Ammann A5 tiles	2	E2	1982		Tilings MLD with Ammann A4.
No image	Penrose hexagon-triangle tiles	3	E2	1997		Uses mirror images of tiles for tiling.
No image	Pegasus tiles	2	E2	2016		Variant of the Penrose hexagon-triangle tiles. Discovered in 2003 or earlier.
	Golden triangle tiles	10	E2	2001		Date is for discovery of matching rules. Dual to Ammann A2.
	Socolar tiles	3	E2	1989		Tilings MLD from the tilings by the Shield tiles.
	Shield tiles	4	E2	1988		Tilings MLD from the tilings by the Socolar tiles.
	Square triangle tiles	5	E2	1986
	Starfish, ivy leaf and hex tiles	3	E2			Tiling is MLD to Penrose P1, P2, P3, and Robinson triangles.
	Robinson triangle	4	E2			Tiling is MLD to Penrose P1, P2, P3, and "Starfish, ivy leaf, hex".
	Danzer triangles	6	E2	1996
	Pinwheel tiles		E2	1994		Date is for publication of matching rules.
	Socolar–Taylor tile	1	E2	2010		Not a connected set. Aperiodic hierarchical tiling.
No image	Wang tiles	20426	E2	1966
No image	Wang tiles	104	E2	2008
No image	Wang tiles	52	E2	1971		Tiles enforce aperiodicity by forming an infinite hierarchy of square lattices.
	Wang tiles	32	E2	1986		Locally derivable from the Penrose tiles.
No image	Wang tiles	24	E2	1986		Locally derivable from the A2 tiling.
	Wang tiles	16	E2	1986		Derived from tiling A2 and its Ammann bars.
	Wang tiles	14	E2	1996
	Wang tiles	13	E2	1996
	Wang tiles	11	E2	2015		Smallest aperiodic set of Wang tiles.
No image	Decagonal Sponge tile	1	E2	2002		Porous tile consisting of non-overlapping point sets.
No image	Goodman-Strauss strongly aperiodic tiles	85	H2	2005
No image	Goodman-Strauss strongly aperiodic tiles	26	H2	2005
	Böröczky hyperbolic tile	1	Hn	1974		Only weakly aperiodic.
No image	Schmitt tile	1	E3	1988		Screw-periodic.
	Schmitt–Conway–Danzer tile	1	E3			Screw-periodic and convex.
	Socolar–Taylor tile	1	E3	2010		Periodic in third dimension.
No image	Penrose rhombohedra	2	E3	1981
	Mackay–Amman rhombohedra	4	E3	1981		Icosahedral symmetry. These are decorated Penrose rhombohedra with a matching rule that force aperiodicity.
No image	Wang cubes	21	E3	1996
No image	Wang cubes	18	E3	1999
No image	Danzer tetrahedra	4	E3	1989
	I and L tiles	2	En for all n ≥ 3	1999
Aperiodic monotile construction diagram, based on Smith (2023)	Smith–Myers–Kaplan–Goodman-Strauss or "Hat" polytile	1	E2	2023		Mirrored monotiles, the first example of an "einstein".
Aperiodic monotile construction diagram, based on Smith (2023)	Smith–Myers–Kaplan–Goodman-Strauss or "Spectre" polytile	1	E2	2023		"Strictly chiral" aperiodic monotile, the first example of a real "einstein".
Supertile made of 2 tiles.	TS1	2	E2	2014

External links

• Stephens P. W., Goldman A. I. The Structure of Quasicrystals
• Levine D., Steinhardt P. J. Quasicrystals I Definition and structure
• Tilings Encyclopedia