Laughlin wavefunction

In condensed matter physics, the Laughlin wavefunction is an ansatz, proposed by Robert Laughlin for the ground state of a two-dimensional electron gas placed in a uniform background magnetic field in the presence of a uniform jellium background when the filling factor of the lowest Landau level is $\nu =1/n$ where $n$ is an odd positive integer. It was constructed to explain the observation of the $\nu =1/3$ fractional quantum Hall effect (FQHE), and predicted the existence of additional $\nu =1/n$ states as well as quasiparticle excitations with fractional electric charge $e/n$, both of which were later experimentally observed. Laughlin received one third of the Nobel Prize in Physics in 1998 for this discovery.

Context and analytical expression

If we ignore the jellium and mutual Coulomb repulsion between the electrons as a zeroth order approximation, we have an infinitely degenerate lowest Landau level (LLL) and with a filling factor of 1/n, we'd expect that all of the electrons would lie in the LLL. Turning on the interactions, we can make the approximation that all of the electrons lie in the LLL. If ${\psi }_0$ is the single particle wavefunction of the LLL state with the lowest orbital angular momenta, then the Laughlin ansatz for the multiparticle wavefunction is

$⟨z_1,z_2,z_3,\dots ,z_N\mid n,N⟩={\psi }_{n,N}(z_1,z_2,z_3,\dots ,z_N)=D\left[\prod _{N⩾i>j⩾1}{(z_i-z_j)}^n\right]\prod _{k=1}^N\exp (-\mid z_k{\mid }^2)$

where position is denoted by

$z=\frac{1}{2{𝑙}_B}(x+iy)$

in (Gaussian units)

${𝑙}_B=\sqrt{\frac{\hslash c}{eB}}$

and $x$ and $y$ are coordinates in the x–y plane. Here $\hslash$ is the reduced Planck constant, $e$ is the electron charge, $N$ is the total number of particles, and $B$ is the magnetic field, which is perpendicular to the xy plane. The subscripts on z identify the particle. In order for the wavefunction to describe fermions, n must be an odd integer. This forces the wavefunction to be antisymmetric under particle interchange. The angular momentum for this state is $n\hslash$.

True ground state in FQHE at ν = 1/3

Consider $n=3$ above: resultant ${\mathrm{\Psi }}_L(z_1,z_2,z_3,\dots ,z_N)\propto {\mathrm{\Pi }}_{i<j}(z_i-z_j{)}^3$ is a trial wavefunction; it is not exact, but qualitatively, it reproduces many features of the exact solution and quantitatively, it has very high overlaps with the exact ground state for small systems. Assuming Coulomb repulsion between any two electrons, that ground state ${\mathrm{\Psi }}_{ED}$ can be determined using exact diagonalisation and the overlaps have been calculated to be close to one. Moreover, with short-range interaction (Haldane pseudopotentials for $m>3$ set to zero), Laughlin wavefunction becomes exact, i.e. $⟨{\mathrm{\Psi }}_{ED}|{\mathrm{\Psi }}_L⟩=1$.

Energy of interaction for two particles

Figure 1. Interaction energy vs. $𝑙$ for $n=7$ and $k_B{r}_B=20$. The energy is in units of $\frac{e^2}{L_B}$. Note that the minima occur for $𝑙=3$ and $𝑙=4$. In general the minima occur at $\frac{𝑙}{n}=\frac{1}{2}\pm \frac{1}{2n}$.

The Laughlin wavefunction is the multiparticle wavefunction for quasiparticles. The expectation value of the interaction energy for a pair of quasiparticles is

$⟨V⟩=⟨n,N\mid V\mid n,N⟩,N=2$

where the screened potential is (see Template:Slink)

$V\left(r_{12}\right)=\left(\frac{2e^2}{L_B}\right)\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{kdk}{k^2+k_B^2{r}_B^2}M(𝑙+1,1,-\frac{k^2}{4})M({𝑙}^{\prime }+1,1,-\frac{k^2}{4}){𝒥}_0\left(k\frac{r_{12}}{r_B}\right)$

where $M$ is a confluent hypergeometric function and ${𝒥}_0$ is a Bessel function of the first kind. Here, $r_{12}$ is the distance between the centers of two current loops, $e$ is the magnitude of the electron charge, $r_B=\sqrt{2}{𝑙}_B$ is the quantum version of the Larmor radius, and $L_B$ is the thickness of the electron gas in the direction of the magnetic field. The angular momenta of the two individual current loops are $𝑙\hslash$ and ${𝑙}^{\prime }\hslash$ where $𝑙+{𝑙}^{\prime }=n$. The inverse screening length is given by (Gaussian units)

$k_B^2=\frac{4\pi e^2}{\hslash {\omega }_{c}A{L}_B}$

where ${\omega }_c$ is the cyclotron frequency, and $A$ is the area of the electron gas in the xy plane.

The interaction energy evaluates to:

$E=\left(\frac{2e^2}{L_B}\right)\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{kdk}{k^2+k_B^2{r}_B^2}M(𝑙+1,1,-\frac{k^2}{4})M({𝑙}^{\prime }+1,1,-\frac{k^2}{4})M(n+1,1,-\frac{k^2}{2})$

Figure 2. Interaction energy vs. $n$ for $\frac{𝑙}{n}=\frac{1}{2}\pm \frac{1}{2n}$ and $k_B{r}_B=0.1,1.0,10$. The energy is in units of $\frac{e^2}{L_B}$.

To obtain this result we have made the change of integration variables

$u_{12}=\frac{z_1-z_2}{\sqrt{2}}$

and

$v_{12}=\frac{z_1+z_2}{\sqrt{2}}$

and noted (see Common integrals in quantum field theory)

$\frac{1}{{\left(2\pi \right)}^2{2}^{2n}n!}\int d^2{z}_1{d}^2{z}_2\mid z_1-z_2{\mid }^{2n}\exp [-2(\mid z_1{\mid }^2+\mid z_2{\mid }^2)]{𝒥}_0\left(\sqrt{2}k\mid z_1-z_2\mid \right)=$

$\frac{1}{{\left(2\pi \right)}^2{2}^{n}n!}\int d^2{u}_{12}{d}^2{v}_{12}\mid u_{12}{\mid }^{2n}\exp [-2(\mid u_{12}{\mid }^2+\mid v_{12}{\mid }^2)]{𝒥}_0(2k\mid u_{12}\mid )=$

$M(n+1,1,-\frac{k^2}{2}).$

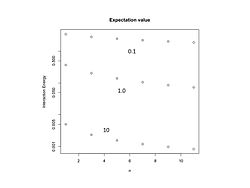
The interaction energy has minima for (Figure 1)

$\frac{𝑙}{n}=\frac{1}{3},\frac{2}{5},\frac{3}{7},\text{etc.,}$

and

$\frac{𝑙}{n}=\frac{2}{3},\frac{3}{5},\frac{4}{7},\text{etc.}$

For these values of the ratio of angular momenta, the energy is plotted in Figure 2 as a function of $n$.

See also

• Landau level
• Fractional quantum Hall effect
• Coulomb potential between two current loops embedded in a magnetic field