Kovasznay flow

Normalized streamline ($\psi /LU$) contours of the Kovasznay flow for $Re=50$. Color contours denote normalized vorticity $\omega L/U$.

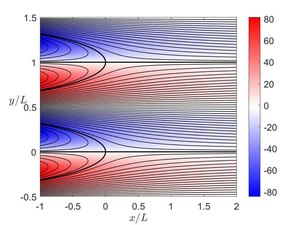
Kovasznay flow corresponds to an exact solution of the Navier–Stokes equations and are interpreted to describe the flow behind a two-dimensional grid. The flow is named after Leslie Stephen George Kovasznay, who discovered this solution in 1948. The solution is often used to validate numerical codes solving two-dimensional Navier-Stokes equations.

Flow description

Let $U$ be the free stream velocity and let $L$ be the spacing between a two-dimensional grid. The velocity field $(u,v,0)$ of the Kovaszany flow, expressed in the Cartesian coordinate system is given by

$\frac{u}{U}=1-e^{\lambda x/L}\cos \left(\frac{2\pi y}{L}\right),\frac{v}{U}=\frac{\lambda }{2\pi }{e}^{\lambda x/L}\sin \left(\frac{2\pi y}{L}\right)$

where $\lambda$ is the root of the equation ${\lambda }^2-Re\lambda -4{\pi }^2=0$ in which $Re=UL/\nu$ represents the Reynolds number of the flow. The root that describes the flow behind the two-dimensional grid is found to be

$\lambda =\frac{1}{2}(Re-\sqrt{R{e}^2+16{\pi }^2}).$

The corresponding vorticity field $(0,0,\omega )$ and the stream function $\psi$ are given by

$\frac{\omega }{U/L}=Re\lambda e^{\lambda x/L}\sin \left(\frac{2\pi y}{L}\right),\frac{\psi }{LU}=\frac{y}{L}-\frac{1}{2\pi }{e}^{\lambda x/L}\sin \left(\frac{2\pi y}{L}\right).$

Similar exact solutions, extending Kovasznay's, has been noted by Lin and Tobak and C. Y. Wang.