Influential observation

In Anscombe's quartet the two datasets on the bottom both contain influential points. All four sets are identical when examined using simple summary statistics, but vary considerably when graphed. If one point is removed, the line would look very different.

In statistics, an influential observation is an observation for a statistical calculation whose deletion from the dataset would noticeably change the result of the calculation. In particular, in regression analysis an influential observation is one whose deletion has a large effect on the parameter estimates.

Assessment

Various methods have been proposed for measuring influence. Assume an estimated regression $𝐲=𝐗𝐛+𝐞$, where $𝐲$ is an n×1 column vector for the response variable, $𝐗$ is the n×k design matrix of explanatory variables (including a constant), $𝐞$ is the n×1 residual vector, and $𝐛$ is a k×1 vector of estimates of some population parameter $\mathit{\beta }\in {ℝ}^k$. Also define $𝐇\equiv 𝐗{\left({𝐗}^{𝖳}𝐗\right)}^{-1}{𝐗}^{𝖳}$, the projection matrix of $𝐗$. Then we have the following measures of influence:

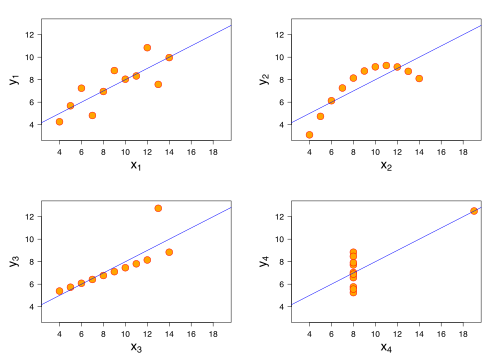
1. ${\text{DFBETA}}_i\equiv 𝐛-{𝐛}_{(-i)}=\frac{{\left({𝐗}^{𝖳}𝐗\right)}^{-1}{𝐱}_i^{𝖳}{e}_i}{1-h_{ii}}$, where ${𝐛}_{(-i)}$ denotes the coefficients estimated with the i-th row ${𝐱}_i$ of $𝐗$ deleted, $h_{ii}={𝐱}_i{\left({𝐗}^{𝖳}𝐗\right)}^{-1}{𝐱}_i^{𝖳}$ denotes the i-th value of matrix's $𝐇$ main diagonal. Thus DFBETA measures the difference in each parameter estimate with and without the influential point. There is a DFBETA for each variable and each observation (if there are N observations and k variables there are N·k DFBETAs). Table shows DFBETAs for the third dataset from Anscombe's quartet (bottom left chart in the figure):

x	y	intercept	slope
10.0	7.46	-0.005	-0.044
8.0	6.77	-0.037	0.019
13.0	12.74	-357.910	525.268
9.0	7.11	-0.033	0
11.0	7.81	0.049	-0.117
14.0	8.84	0.490	-0.667
6.0	6.08	0.027	-0.021
4.0	5.39	0.241	-0.209
12.0	8.15	0.137	-0.231
7.0	6.42	-0.020	0.013
5.0	5.73	0.105	-0.087

Outliers, leverage and influence

An outlier may be defined as a data point that differs markedly from other observations. A high-leverage point are observations made at extreme values of independent variables. Both types of atypical observations will force the regression line to be close to the point. In Anscombe's quartet, the bottom right image has a point with high leverage and the bottom left image has an outlying point.

See also

• Influence function (statistics)
• Outlier
• Leverage
  • Partial leverage
• Regression analysis
• Template:Slink
• Anomaly detection

Further reading

• Template:Cite journal
• Template:Cite book