Eight-vertex model

Template:Short description In statistical mechanics, the eight-vertex model is a generalization of the ice-type (six-vertex) models. It was discussed by Sutherland and Fan & Wu, and solved by Rodney Baxter in the zero-field case.

Description

As with the ice-type models, the eight-vertex model is a square lattice model, where each state is a configuration of arrows at a vertex. The allowed vertices have an even number of arrows pointing towards the vertex; these include the six inherited from the ice-type model (1-6), sinks (7), and sources (8).

The eight allowed vertices.

We consider a $N\times N$ lattice, with $N^2$ vertices and $2N^2$ edges. Imposing periodic boundary conditions requires that the states 7 and 8 occur equally often, as do states 5 and 6, and thus can be taken to have the same energy. For the zero-field case the same is true for the two other pairs of states. Each vertex $j$ has an associated energy ${ϵ}_j$ and Boltzmann weight

$w_j=\exp (-\frac{{ϵ}_j}{k_{\mathrm{B}}T})$

giving the partition function over the lattice as

$Z=\sum \exp (-\frac{\sum _j{n}_j{ϵ}_j}{k_{\mathrm{B}}T})$

where the outer summation is over all allowed configurations of vertices in the lattice. In this general form the partition function remains unsolved.

Solution in the zero-field case

The zero-field case of the model corresponds physically to the absence of external electric fields. Hence, the model remains unchanged under the reversal of all arrows. The states 1 and 2, and 3 and 4, consequently must occur as pairs. The vertices may be assigned arbitrary weights

$\begin{array}{cc}{w}_1=w_2& =a\\ w_3=w_4& =b\\ w_5=w_6& =c\\ w_7=w_8& =d.\end{array}$

The solution is based on the observation that rows in transfer matrices commute, for a certain parametrization of these four Boltzmann weights. This came about as a modification of an alternate solution for the six-vertex model which makes use of elliptic theta functions.

Commuting transfer matrices

The proof relies on the fact that when ${\mathrm{\Delta }}^{\prime }=\mathrm{\Delta }$ and ${\mathrm{\Gamma }}^{\prime }=\mathrm{\Gamma }$, for quantities

$\begin{array}{cc}\mathrm{\Delta }& =\frac{a^2+b^2-c^2-d^2}{2(ab+cd)}\\ \mathrm{\Gamma }& =\frac{ab-cd}{ab+cd}\end{array}$

the transfer matrices $T$ and $T^{\prime }$ (associated with the weights $a$, $b$, $c$, $d$ and $a^{\prime }$, $b^{\prime }$, $c^{\prime }$, $d^{\prime }$) commute. Using the star-triangle relation, Baxter reformulated this condition as equivalent to a parametrization of the weights given as

$a:b:c:d=\mathrm{snh}(\eta -u):\mathrm{snh}(\eta +u):\mathrm{snh}(2\eta ):k\mathrm{snh}(2\eta )\mathrm{snh}(\eta -u)\mathrm{snh}(\eta +u)$

for fixed modulus $k$ and $\eta$ and variable $u$. Here snh is the hyperbolic analogue of sn, given by

$\begin{array}{cc}\mathrm{snh}(u)& =-i\mathrm{sn}(iu)=i\mathrm{sn}(-iu)\\ \text{where }\mathrm{sn}(u)& =\frac{H(u)}{\sqrt{k}\mathrm{\Theta }(u)}\end{array}$

and $H(u)$ and $\mathrm{\Theta }(u)$ are theta functions of modulus $k$. The associated transfer matrix $T$ thus is a function of $u$ alone; for all $u$, $v$

$T(u)T(v)=T(v)T(u).$

The matrix function $Q(u)$

The other crucial part of the solution is the existence of a nonsingular matrix-valued function $Q$, such that for all complex $u$ the matrices $Q(u),Q(u^{\prime })$ commute with each other and the transfer matrices, and satisfy Template:NumBlk where

$\begin{array}{cc}\zeta (u)& =[c^{-1}H(2\eta )\mathrm{\Theta }(u-\eta )\mathrm{\Theta }(u+\eta ){]}^N\\ \varphi (u)& =[\mathrm{\Theta }(0)H(u)\mathrm{\Theta }(u){]}^N.\end{array}$

The existence and commutation relations of such a function are demonstrated by considering pair propagations through a vertex, and periodicity relations of the theta functions, in a similar way to the six-vertex model.

Explicit solution

The commutation of matrices in (Template:EquationNote) allow them to be diagonalised, and thus eigenvalues can be found. The partition function is calculated from the maximal eigenvalue, resulting in a free energy per site of

$\begin{array}{c}f={ϵ}_5-2kT\sum _{n=1}^{\mathrm{\infty }}\frac{{\sinh }^2((\tau -\lambda )n)(\cosh (n\lambda )-\cosh (n\alpha ))}{n\sinh (2n\tau )\cosh (n\lambda )}\end{array}$

for

$\begin{array}{cc}\tau & =\frac{\pi K^{\prime }}{2K}\\ \lambda & =\frac{\pi \eta }{iK}\\ \alpha & =\frac{\pi u}{iK}\end{array}$

where $K$ and $K^{\prime }$ are the complete elliptic integrals of moduli $k$ and $k^{\prime }$. The eight vertex model was also solved in quasicrystals.

Equivalence with an Ising model

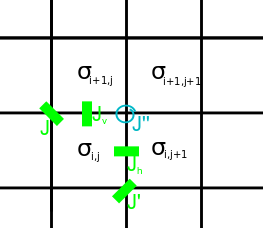
There is a natural correspondence between the eight-vertex model, and the Ising model with 2-spin and 4-spin nearest neighbor interactions. The states of this model are spins $\sigma =\pm 1$ on faces of a square lattice. The analogue of 'edges' in the eight-vertex model are products of spins on adjacent faces:

$\begin{array}{cc}{\alpha }_{ij}& ={\sigma }_{ij}{\sigma }_{i,j+1}\\ {\mu }_{ij}& ={\sigma }_{ij}{\sigma }_{i+1,j}.\end{array}$

The most general form of the energy for this model is

$\begin{array}{cc}ϵ& =-\sum _{ij}(J_h{\mu }_{ij}+J_v{\alpha }_{ij}+J{\alpha }_{ij}{\mu }_{ij}+J^{\prime }{\alpha }_{i+1,j}{\mu }_{ij}+J^{″}{\alpha }_{ij}{\alpha }_{i+1,j})\end{array}$

where $J_h$, $J_v$, $J$, $J^{\prime }$ describe the horizontal, vertical and two diagonal 2-spin interactions, and $J^{″}$ describes the 4-spin interaction between four faces at a vertex; the sum is over the whole lattice.

We denote horizontal and vertical spins (arrows on edges) in the eight-vertex model $\mu$, $\alpha$ respectively, and define up and right as positive directions. The restriction on vertex states is that the product of four edges at a vertex is 1; this automatically holds for Ising "edges." Each $\sigma$ configuration then corresponds to a unique $\mu$, $\alpha$ configuration, whereas each $\mu$, $\alpha$ configuration gives two choices of $\sigma$ configurations.

Equating general forms of Boltzmann weights for each vertex $j$, the following relations between the ${ϵ}_j$ and $J_h$, $J_v$, $J$, $J^{\prime }$, $J^{″}$ define the correspondence between the lattice models:

$\begin{array}{cc}{ϵ}_1& =-J_h-J_v-J-J^{\prime }-J^{″},{ϵ}_2=J_h+J_v-J-J^{\prime }-J^{″}\\ {ϵ}_3& =-J_h+J_v+J+J^{\prime }-J^{″},{ϵ}_4=J_h-J_v+J+J^{\prime }-J^{″}\\ {ϵ}_5& ={ϵ}_6=J-J^{\prime }+J^{″}\\ {ϵ}_7& ={ϵ}_8=-J+J^{\prime }+J^{″}.\end{array}$

It follows that in the zero-field case of the eight-vertex model, the horizontal and vertical interactions in the corresponding Ising model vanish.

These relations gives the equivalence $Z_I=2Z_{8V}$ between the partition functions of the eight-vertex model, and the (2,4)-spin Ising model. Consequently a solution in either model would lead immediately to a solution in the other.

See also

• Six-vertex model
• Transfer-matrix method
• Ising model

References

• Template:Citation