Convection–diffusion equation

Template:Short description The convection–diffusion equation is a parabolic partial differential equation that combines the diffusion and convection (advection) equations. It describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift–diffusion equation, or (generic) scalar transport equation.

Equation

A contaminant plume moving in porous media via the Convection–Diffusion Equation (also called Advective–Diffusion Equation) (time stamps of 1 day, 85 days, 462 days and 674 days) with advection as primary transport mechanism.

The general equation in conservative form isTemplate:Sfn $$\frac{\partial c}{\partial t}=\mathrm{\nabla }\cdot (D\mathrm{\nabla }c-𝐯c)+R$$ where

• Template:Mvar is the variable of interest (species concentration for mass transfer, temperature for heat transfer),
• Template:Mvar is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport,
• Template:Math is the velocity field that the quantity is moving with. It is a function of time and space. For example, in advection, Template:Mvar might be the concentration of salt in a river, and then Template:Math would be the velocity of the water flow as a function of time and location. Another example, Template:Mvar might be the concentration of small bubbles in a calm lake, and then Template:Math would be the velocity of bubbles rising towards the surface by buoyancy (see below) depending on time and location of the bubble. For multiphase flows and flows in porous media, Template:Math is the (hypothetical) superficial velocity.
• Template:Mvar describes sources or sinks of the quantity Template:Mvar, i.e. the creation or destruction of the quantity. For example, for a chemical species, Template:Math means that a chemical reaction is creating more of the species, and Template:Math means that a chemical reaction is destroying the species. For heat transport, Template:Math might occur if thermal energy is being generated by friction.
• Template:Math represents gradient and Template:Math represents divergence. In this equation, Template:Math represents concentration gradient.

In general, Template:Mvar, Template:Math, and Template:Mvar may vary with space and time. In cases in which they depend on concentration as well, the equation becomes nonlinear, giving rise to many distinctive mixing phenomena such as Rayleigh–Bénard convection when Template:Math depends on temperature in the heat transfer formulation and reaction–diffusion pattern formation when Template:Mvar depends on concentration in the mass transfer formulation.

Often there are several quantities, each with its own convection–diffusion equation, where the destruction of one quantity entails the creation of another. For example, when methane burns, it involves not only the destruction of methane and oxygen but also the creation of carbon dioxide and water vapor. Therefore, while each of these chemicals has its own convection–diffusion equation, they are coupled together and must be solved as a system of differential equations.

Derivation

The convection–diffusion equation can be derived in a straightforward way from the continuity equation, which states that the rate of change for a scalar quantity in a differential control volume is given by flow and diffusion into and out of that part of the system along with any generation or consumption inside the control volume: $$\frac{\partial c}{\partial t}+\mathrm{\nabla }\cdot 𝐣=R,$$ where Template:Math is the total flux and Template:Mvar is a net volumetric source for Template:Mvar. There are two sources of flux in this situation. First, diffusive flux arises due to diffusion. This is typically approximated by Fick's first law: $${𝐣}_{\text{diff}}=-D\mathrm{\nabla }c$$ i.e., the flux of the diffusing material (relative to the bulk motion) in any part of the system is proportional to the local concentration gradient. Second, when there is overall convection or flow, there is an associated flux called advective flux: $${𝐣}_{\text{adv}}=𝐯c$$ The total flux (in a stationary coordinate system) is given by the sum of these two: $$𝐣={𝐣}_{\text{diff}}+{𝐣}_{\text{adv}}=-D\mathrm{\nabla }c+𝐯c.$$ Plugging into the continuity equation: $$\frac{\partial c}{\partial t}+\mathrm{\nabla }\cdot (-D\mathrm{\nabla }c+𝐯c)=R.$$

Common simplifications

In a common situation, the diffusion coefficient is constant, there are no sources or sinks, and the velocity field describes an incompressible flow (i.e., it has zero divergence). Then the formula simplifies to: $$\frac{\partial c}{\partial t}=D{\mathrm{\nabla }}^{2}c-𝐯\cdot \mathrm{\nabla }c.$$

In this case the equation can be put in the simple diffusion form: $$\frac{dc}{dt}=D{\mathrm{\nabla }}^{2}c,$$

where the derivative of the left hand side is the material derivative of the variable c. In non-interacting material, Template:Mvar (for example, when temperature is close to absolute zero, dilute gas has almost zero mass diffusivity), hence the transport equation is simply the continuity equation: $$\frac{\partial c}{\partial t}+𝐯\cdot \mathrm{\nabla }c=0.$$

Using Fourier transform in both temporal and spatial domain (that is, with integral kernel $e^{i\omega t+i𝐤\cdot 𝐱}$), its characteristic equation can be obtained: $$i\omega \tilde{c}+𝐯\cdot i𝐤\tilde{c}=0\to \omega =-𝐤\cdot 𝐯,$$ which gives the general solution: $$c=f(𝐱-𝐯t),$$ where $f$ is any differentiable scalar function. This is the basis of temperature measurement for near Bose–Einstein condensate via time of flight method.

Stationary version

The stationary convection–diffusion equation describes the steady-state behavior of a convection–diffusion system.Template:Sfn In a steady state, Template:Math, so the equation to solve becomes the second order equation: $$\mathrm{\nabla }\cdot (-D\mathrm{\nabla }c+𝐯c)=R.$$ In one spatial dimension, the equation can be written as $$\frac{d}{dx}(-D(x)\frac{dc(x)}{dx}+v(x)c(x))=R(x)$$

Which can be integrated one time in the space variable x to give:

$$D(x)\frac{dc(x)}{dx}-v(x)c(x)=-\underset{x}{\int }R(x^{\prime })d{x}^{\prime }$$

Where D is not zero, this is an inhomogeneous first-order linear differential equation with variable coefficients in the variable c(x):

$$y^{\prime }(x)=f(x)y(x)+g(x).$$ where the coefficients are: $$f(x)=\frac{v(x)}{D(x)}$$ and: $$g(x)=-\frac{1}{D(x)}\underset{x}{\int }R(x^{\prime })d{x}^{\prime }$$ On the other hand, in the positions x where D=0, the first-order diffusion term disappears and the solution becomes simply the ratio:

$$c(x)=\frac{1}{v(x)}\underset{x}{\int }R(x^{\prime })d{x}^{\prime }$$

Velocity in response to a force

In some cases, the average velocity field Template:Math exists because of a force; for example, the equation might describe the flow of ions dissolved in a liquid, with an electric field pulling the ions in some direction (as in gel electrophoresis). In this situation, it is usually called the drift–diffusion equation or the Smoluchowski equation, after Marian Smoluchowski who described it in 1915 (not to be confused with the Einstein–Smoluchowski relation or Smoluchowski coagulation equation).

Typically, the average velocity is directly proportional to the applied force, giving the equation: $$\frac{\partial c}{\partial t}=\mathrm{\nabla }\cdot (D\mathrm{\nabla }c)-\mathrm{\nabla }\cdot \left({\zeta }^{-1}𝐅c\right)+R$$ where Template:Math is the force, and Template:Mvar characterizes the friction or viscous drag. (The inverse Template:Math is called mobility.)

Derivation of Einstein relation

When the force is associated with a potential energy Template:Math (see conservative force), a steady-state solution to the above equation (i.e. Template:Math) is: $$c\propto \exp (-D^{-1}{\zeta }^{-1}U)$$ (assuming Template:Mvar and Template:Mvar are constant). In other words, there are more particles where the energy is lower. This concentration profile is expected to agree with the Boltzmann distribution (more precisely, the Gibbs measure). From this assumption, the Einstein relation can be proven: $$D\zeta =k_{\mathrm{B}}T.$$

Similar equations in other contexts

The convection–diffusion equation is a relatively simple equation describing flows, or alternatively, describing a stochastically-changing system. Therefore, the same or similar equation arises in many contexts unrelated to flows through space.

• It is formally identical to the Fokker–Planck equation for the velocity of a particle.
• It is closely related to the Black–Scholes equation and other equations in financial mathematics.
• It is closely related to the Navier–Stokes equations, because the flow of momentum in a fluid is mathematically similar to the flow of mass or energy. The correspondence is clearest in the case of an incompressible Newtonian fluid, in which case the Navier–Stokes equation is: $$\frac{\partial 𝐌}{\partial t}=\mu {\mathrm{\nabla }}^2𝐌-𝐯\cdot \mathrm{\nabla }𝐌+(𝐟-\mathrm{\nabla }P)$$

where Template:Math is the momentum of the fluid (per unit volume) at each point (equal to the density Template:Mvar multiplied by the velocity Template:Math), Template:Mvar is viscosity, Template:Mvar is fluid pressure, and Template:Math is any other body force such as gravity. In this equation, the term on the left-hand side describes the change in momentum at a given point; the first term on the right describes the diffusion of momentum by viscosity; the second term on the right describes the advective flow of momentum; and the last two terms on the right describes the external and internal forces which can act as sources or sinks of momentum.

In probability theory

The convection–diffusion equation (with Template:Math) can be viewed as a stochastic differential equation, describing random motion with diffusivity Template:Mvar and bias Template:Math. For example, the equation can describe the Brownian motion of a single particle, where the variable Template:Mvar describes the probability distribution for the particle to be in a given position at a given time. The reason the equation can be used that way is because there is no mathematical difference between the probability distribution of a single particle, and the concentration profile of a collection of infinitely many particles (as long as the particles do not interact with each other).

The Langevin equation describes advection, diffusion, and other phenomena in an explicitly stochastic way. One of the simplest forms of the Langevin equation is when its "noise term" is Gaussian; in this case, the Langevin equation is exactly equivalent to the convection–diffusion equation. However, the Langevin equation is more general.

In semiconductor physics

As carriers are generated (green:electrons and purple:holes) due to light shining at the center of an intrinsic semiconductor, they diffuse towards two ends. Electrons have higher diffusion constant than holes leading to fewer excess electrons at the center as compared to holes.

In semiconductor physics, this equation is called the drift–diffusion equation. The word "drift" is related to drift current and drift velocity. The equation is normally written: $$\begin{array}{cc}\frac{{𝐉}_n}{-q}& =-D_n\mathrm{\nabla }n-n{\mu }_n𝐄\\ \frac{{𝐉}_p}{q}& =-D_p\mathrm{\nabla }p+p{\mu }_p𝐄\\ \frac{\partial n}{\partial t}& =-\mathrm{\nabla }\cdot \frac{{𝐉}_n}{-q}+R\\ \frac{\partial p}{\partial t}& =-\mathrm{\nabla }\cdot \frac{{𝐉}_p}{q}+R\end{array}$$ where

• Template:Mvar and Template:Mvar are the concentrations (densities) of electrons and holes, respectively,
• Template:Math is the elementary charge,
• Template:Mvar and Template:Mvar are the electric currents due to electrons and holes respectively,
• Template:Math and Template:Math are the corresponding "particle currents" of electrons and holes respectively,
• Template:Mvar represents carrier generation and recombination (Template:Math for generation of electron-hole pairs, Template:Math for recombination.)
• Template:Math is the electric field vector
• ${\mu }_n$ and ${\mu }_p$ are electron and hole mobility.

The diffusion coefficient and mobility are related by the Einstein relation as above: $$\begin{array}{cc}{D}_n& =\frac{{\mu }_n{k}_{\mathrm{B}}T}{q},\\ D_p& =\frac{{\mu }_p{k}_{\mathrm{B}}T}{q},\end{array}$$ where Template:Math is the Boltzmann constant and Template:Mvar is absolute temperature. The drift current and diffusion current refer separately to the two terms in the expressions for Template:Math, namely: $$\begin{array}{cc}\frac{{𝐉}_{n,\text{drift}}}{-q}& =-n{\mu }_n𝐄,\\ \frac{{𝐉}_{p,\text{drift}}}{q}& =p{\mu }_p𝐄,\\ \frac{{𝐉}_{n,\text{diff}}}{-q}& =-D_n\mathrm{\nabla }n,\\ \frac{{𝐉}_{p,\text{diff}}}{q}& =-D_p\mathrm{\nabla }p.\end{array}$$

This equation can be solved together with Poisson's equation numerically.

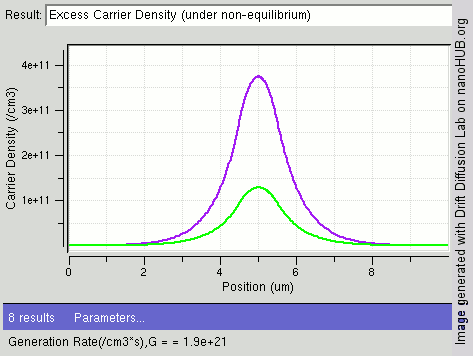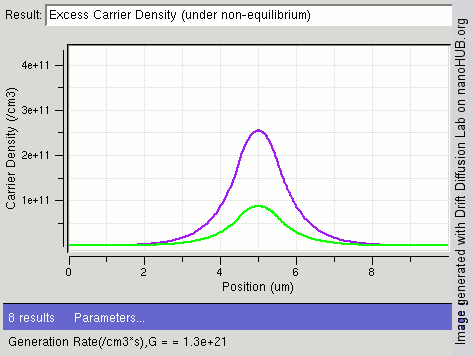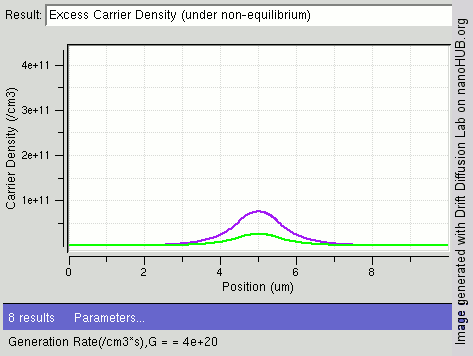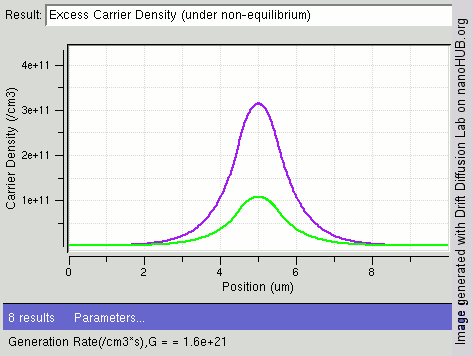
An example of results of solving the drift diffusion equation is shown on the right. When light shines on the center of semiconductor, carriers are generated in the middle and diffuse towards two ends. The drift–diffusion equation is solved in this structure and electron density distribution is displayed in the figure. One can see the gradient of carrier from center towards two ends.

See also

• Advanced Simulation Library
• Buckley–Leverett equation
• Burgers' equation
• Conservation equations
• Double diffusive convection
• Incompressible Navier–Stokes equations
• Natural convection
• Nernst–Planck equation
• Numerical solution of the convection–diffusion equation

References

• Template:Cite book

Further reading

• Template:Cite book