Complexity index

Template:Multiple issues In modern computer science and statistics, the complexity index of a function denotes the level of informational content, which in turn affects the difficulty of learning the function from examples. This is different from computational complexity, which is the difficulty to compute a function. Complexity indices characterize the entire class of functions to which the one we are interested in belongs. Focusing on Boolean functions, the detail of a class $𝖢$ of Boolean functions c essentially denotes how deeply the class is articulated.

Technical definition

To identify this index we must first define a sentry function of $𝖢$. Let us focus for a moment on a single function c, call it a concept defined on a set $𝒳$ of elements that we may figure as points in a Euclidean space. In this framework, the above function associates to c a set of points that, since are defined to be external to the concept, prevent it from expanding into another function of $𝖢$. We may dually define these points in terms of sentinelling a given concept c from being fully enclosed (invaded) by another concept within the class. Therefore, we call these points either sentinels or sentry points; they are assigned by the sentry function $𝑺$ to each concept of $𝖢$ in such a way that:

1. the sentry points are external to the concept c to be sentineled and internal to at least one other including it,
2. each concept $c^{\prime }$ including c has at least one of the sentry points of c either in the gap between c and $c^{\prime }$, or outside $c^{\prime }$ and distinct from the sentry points of $c^{\prime }$, and
3. they constitute a minimal set with these properties.

The technical definition coming from Template:Harv is rooted in the inclusion of an augmented concept $c^{+}$ made up of c plus its sentry points by another ${\left(c^{\prime }\right)}^{+}$ in the same class.

Definition of sentry function

For a concept class $𝖢$ on a space $𝔛$, a sentry function is a total function $𝑺:𝖢\cup \{\mathrm{\varnothing },𝔛\}\mapsto 2^{𝔛}$ satisfying the following conditions:

1. Sentinels are outside the sentineled concept ($c\cap 𝑺(c)=\mathrm{\varnothing }$ for all $c\in 𝖢$).
2. Sentinels are inside the invading concept (Having introduced the sets $c^{+}=c\cup 𝑺(c)$, an invading concept $c^{\prime }\in 𝖢$ is such that $c^{\prime }\subseteq ̸c$ and $c^{+}\subseteq {\left(c^{\prime }\right)}^{+}$. Denoting $\mathrm{u}\mathrm{p}(c)$ the set of concepts invading c, we must have that if $c_2\in \mathrm{u}\mathrm{p}(c_1)$, then $c_2\cap 𝑺(c_1)\ne \mathrm{\varnothing }$).
3. $𝑺(c)$ is a minimal set with the above properties (No $𝑺\text{'}\ne 𝑺$ exists satisfying (1) and (2) and having the property that ${𝑺}^{\prime }(c)\subseteq 𝑺(c)$ for every $c\in 𝖢$).
4. Sentinels are honest guardians. It may be that $c\subseteq {\left(c^{\prime }\right)}^{+}$ but $𝑺(c)\cap c^{\prime }=\mathrm{\varnothing }$ so that $c^{\prime }\in ̸\mathrm{u}\mathrm{p}(c)$. This however must be a consequence of the fact that all points of $𝑺(c)$ are involved in really sentineling c against other concepts in $\mathrm{u}\mathrm{p}(c)$ and not just in avoiding inclusion of $c^{+}$ by $(c^{\prime }{)}^{+}$. Thus if we remove $c^{\prime },𝑺(c)$ remains unchanged (Whenever $c_1$ and $c_2$ are such that $c_1\subset c_2\cup 𝑺(c_2)$ and $c_2\cap 𝑺(c_1)=\mathrm{\varnothing }$, then the restriction of $𝑺$ to $\{c_1\}\cup \mathrm{u}\mathrm{p}(c_1)-\{c_2\}$ is a sentry function on this set).

$𝑺(c)$ is the frontier of c upon $𝑺$.

A schematic outlook of outer sentineling functionality

With reference to the picture on the right, $\{x_1,x_2,x_3\}$ is a candidate frontier of $c_0$ against $c_1,c_2,c_3,c_4$. All points are in the gap between a $c_i$ and $c_0$. They avoid inclusion of $c_0\cup \{x_1,x_2,x_3\}$ in $c_3$, provided that these points are not used by the latter for sentineling itself against other concepts. Vice versa we expect that $c_1$ uses $x_1$ and $x_3$ as its own sentinels, $c_2$ uses $x_2$ and $x_3$ and $c_4$ uses $x_1$ and $x_2$ analogously. Point $x_4$ is not allowed as a $c_0$ sentry point since, like any diplomatic seat, it should be located outside all other concepts just to ensure that it is not occupied in case of invasion by $c_0$.

Definition of detail

Template:AnchorThe frontier size of the most expensive concept to be sentineled with the least efficient sentineling function, i.e. the quantity

${\mathrm{D}}_{𝖢}=\underset{𝑺,c}{\sup }\mathrm{\#}𝑺(c)$,

is called detail of $𝖢$. $𝑺$ spans also over sentry functions on subsets of $𝔛$ sentineling in this case the intersections of the concepts with these subsets. Actually, proper subsets of $𝔛$ may host sentineling tasks that prove harder than those emerging with $𝔛$ itself.

The detail ${\mathrm{D}}_{𝖢}$ is a complexity measure of concept classes dual to the VC dimension ${\mathrm{D}}_{𝖵C}$. The former uses points to separate sets of concepts, the latter concepts for partitioning sets of points. In particular the following inequality holds Template:Harv

${\mathrm{D}}_{𝖢}\le {\mathrm{D}}_{𝖵C}+1$

See also Rademacher complexity for a recently introduced class complexity index.

Example: continuous spaces

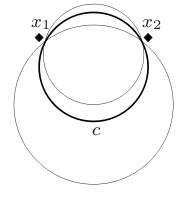
Class C of circles in ${ℝ}^2$ has detail ${\mathrm{D}}_{𝖢}=2$, as shown in the picture on left below. Similarly, for the class of segments on $ℝ$, as shown in the picture on right.

Two points $x_1,x_2$ outside c (thick circle) are sufficient to prevent a larger circle not containing them from including it

The class of segments in $ℝ$ and two points needed to sentinel its concepts

Example: discrete spaces

The class $𝖢=\{c_1,c_2,c_3,c_4\}$ on $𝔛=\{x_1,x_2,x_3\}$ whose concepts are illustrated in the following scheme, where "+" denotes an element $x_j$ belonging to $c_i$, "-" an element outside $c_i$, and ⃝ a sentry point:

	$x_1$	$x_2$	$x_3$
$c_1=$	-⃝	-⃝	-
$c_2=$	-⃝	+	+
$c_3=$	+	-⃝	+
$c_4=$	+	+	+

This class has ${\mathrm{D}}_{𝖢}=2$. As usual we may have different sentineling functions. A worst case Template:Math, as illustrated, is: $𝐒(c_1)=\{x_1,x_2\},𝐒(c_2)=\{x_1\},𝐒(c_3)=\{x_2\},𝐒(c_4)=\mathrm{\varnothing }$. However a cheaper one is $𝐒(c_1)=\{x_3\},𝐒(c_2)=\{x_1\},𝐒(c_3)=\{x_2\},𝐒(c_4)=\mathrm{\varnothing }$:

	$x_1$	$x_2$	$x_3$
$c_1=$	-	-	-⃝
$c_2=$	-⃝	+	+
$c_3=$	+	-⃝	+
$c_4=$	+	+	+

References

• Template:Cite book
• Template:Cite journal