Compact quasi-Newton representation

The compact representation for quasi-Newton methods is a matrix decomposition, which is typically used in gradient based optimization algorithms or for solving nonlinear systems. The decomposition uses a low-rank representation for the direct and/or inverse Hessian or the Jacobian of a nonlinear system. Because of this, the compact representation is often used for large problems and constrained optimization.

The compact representation (right) of a dense Hessian approximation (left) is an initial matrix (typically diagonal) plus low rank decomposition. It has a small memory footprint (shaded areas) and enables efficient matrix computations

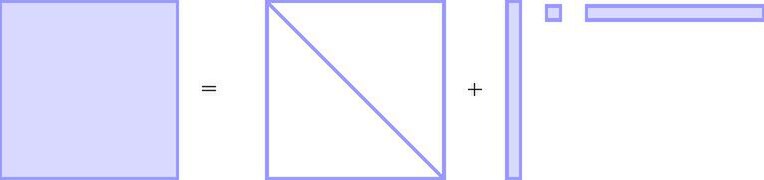
Definition

The compact representation of a quasi-Newton matrix for the inverse Hessian $H_k$ or direct Hessian $B_k$ of a nonlinear objective function $f(x):{ℝ}^n\to ℝ$ expresses a sequence of recursive rank-1 or rank-2 matrix updates as one rank-$k$ or rank-$2k$ update of an initial matrix. Because it is derived from quasi-Newton updates, it uses differences of iterates and gradients $\mathrm{\nabla }f(x_k)=g_k$ in its definition $\{s_{i-1}=x_i-x_{i-1},y_{i-1}=g_i-g_{i-1}{\}}_{i=1}^k$. In particular, for $r=k$ or $r=2k$ the rectangular $n\times r$ matrices $U_k,J_k$ and the $r\times r$ square symmetric systems $M_k,N_k$ depend on the $s_i,y_i$'s and define the quasi-Newton representations

$H_k=H_0+U_k{M}_k^{-1}{U}_k^T,\text{ and }{B}_k=B_0+J_k{N}_k^{-1}{J}_k^T$

Applications

Because of the special matrix decomposition the compact representation is implemented in state-of-the-art optimization software. When combined with limited-memory techniques it is a popular technique for constrained optimization with gradients. Linear algebra operations can be done efficiently, like matrix-vector products, solves or eigendecompositions. It can be combined with line-search and trust region techniques, and the representation has been developed for many quasi-Newton updates. For instance, the matrix vector product with the direct quasi-Newton Hessian and an arbitrary vector $g\in {ℝ}^n$ is:

$\begin{array}{cc}{p}_k^{(0)}& =J_k^{T}g\\ \text{solve}{N}_k{p}_k^{(1)}& =p_k^{(0)}\text{(}{N}_k\text{ is small)}\\ p_k^{(2)}& =J_k{p}_k^{(1)}\\ p_k^{(3)}& =H_{0}g\\ p_k^{\phantom{(4)}}& =p_k^{(2)}+p_k^{(3)}\end{array}$

Background

In the context of the GMRES method, Walker showed that a product of Householder transformations (an identity plus rank-1) can be expressed as a compact matrix formula. This led to the derivation of an explicit matrix expression for the product of $k$ identity plus rank-1 matrices. Specifically, for $S_k=\left[\begin{array}{ccc}{s}_0& s_1& \dots s_{k-1}\end{array}\right],$ $Y_k=\left[\begin{array}{ccc}{y}_0& y_1& \dots y_{k-1}\end{array}\right],$ $(R_k{)}_{ij}=s_{i-1}^T{y}_{j-1},$ ${\rho }_{i-1}=1/s_{i-1}^T{y}_{i-1}$ and $V_i=I-{\rho }_{i-1}{y}_{i-1}{s}_{i-1}^T$ when $1\le i\le j\le k$ the product of $k$ rank-1 updates to the identity is $$\prod _{i=1}^k{V}_{i-1}=(I-{\rho }_0{y}_0{s}_0^T)\cdots (I-{\rho }_{k-1}{y}_{k-1}{s}_{k-1}^T)=I-Y_k{R}_k^{-1}{S}_k^T$$ The BFGS update can be expressed in terms of products of the $V_i$'s, which have a compact matrix formula. Therefore, the BFGS recursion can exploit these block matrix representations

Recursive quasi-Newton updates

A parametric family of quasi-Newton updates includes many of the most known formulas. For arbitrary vectors $v_k$ and $c_k$ such that $v_k^T{y}_k\ne 0$ and $c_k^T{s}_k\ne 0$ general recursive update formulas for the inverse and direct Hessian estimates are Template:NumBlk Template:NumBlk

By making specific choices for the parameter vectors $v_k$ and $c_k$ well known methods are recovered

Table 1: Quasi-Newton updates parametrized by vectors $v_k$ and $c_k$

$v_k$	$\text{method}$	$c_k$	$\text{method}$
$s_k$	BFGS	$s_k$	PSB (Powell Symmetric Broyden)
$y_k$	$\text{Greenstadt's}$	$y_k$	DFP
$s_k-H_k{y}_k$	SR1	$y_k-B_k{s}_k$	SR1
		$P_k^{\text{S}}{s}_k$	MSS (Multipoint-Symmetric-Secant)

Compact Representations

Collecting the updating vectors of the recursive formulas into matrices, define

$$S_k=\left[\begin{array}{cccc}{s}_0& s_1& \dots & s_{k-1}\end{array}\right],$$ $$Y_k=\left[\begin{array}{cccc}{y}_0& y_1& \dots & y_{k-1}\end{array}\right],$$ $$V_k=\left[\begin{array}{cccc}{v}_0& v_1& \dots & v_{k-1}\end{array}\right],$$ $$C_k=\left[\begin{array}{cccc}{c}_0& c_1& \dots & c_{k-1}\end{array}\right],$$

upper triangular

$$(R_k{)}_{ij}:=(R_k^{\text{SY}}{)}_{ij}=s_{i-1}^T{y}_{j-1},(R_k^{\text{VY}}{)}_{ij}=v_{i-1}^T{y}_{j-1},(R_k^{\text{CS}}{)}_{ij}=c_{i-1}^T{s}_{j-1},\text{ for }1\le i\le j\le k$$

lower triangular

$$(L_k{)}_{ij}:=(L_k^{\text{SY}}{)}_{ij}=s_{i-1}^T{y}_{j-1},(L_k^{\text{VY}}{)}_{ij}=v_{i-1}^T{y}_{j-1},(L_k^{\text{CS}}{)}_{ij}=c_{i-1}^T{s}_{j-1},\text{ for }1\le j<i\le k$$

and diagonal

$$(D_k{)}_{ij}:=(D_k^{\text{SY}}{)}_{ij}=s_{i-1}^T{y}_{j-1},\text{ for }1\le i=j\le k$$

With these definitions the compact representations of general rank-2 updates in (Template:EquationNote) and (Template:EquationNote) (including the well known quasi-Newton updates in Table 1) have been developed in Brust:

$$U_k=\left[\begin{array}{cc}{V}_k& S_k-H_0{Y}_k\end{array}\right]$$

$$M_k=\left[\begin{array}{cc}{0}_{k\times k}& R_k^{\text{VY}}\\ (R_k^{\text{VY}}{)}^T& R_k+R_k^T-(D_k+Y_k^T{H}_0{Y}_k)\end{array}\right]$$

and the formula for the direct Hessian is

$$J_k=\left[\begin{array}{cc}{C}_k& Y_k-B_0{S}_k\end{array}\right]$$

$$N_k=\left[\begin{array}{cc}{0}_{k\times k}& R_k^{\text{CS}}\\ (R_k^{\text{CS}}{)}^T& R_k+R_k^T-(D_k+S_k^T{B}_0{S}_k)\end{array}\right]$$

For instance, when $V_k=S_k$ the representation in (Template:EquationNote) is the compact formula for the BFGS recursion in (Template:EquationNote).

Specific Representations

Prior to the development of the compact representations of (Template:EquationNote) and (Template:EquationNote), equivalent representations have been discovered for most known updates (see Table 1).

BFGS

Along with the SR1 representation, the BFGS (Broyden-Fletcher-Goldfarb-Shanno) compact representation was the first compact formula known. In particular, the inverse representation is given by

$H_k=H_0+U_k{M}_k^{-1}{U}_k^T,U_k=\left[\begin{array}{cc}{S}_k& H_0{Y}_k\end{array}\right],M_k^{-1}=\left[\begin{array}{cc}{R}_k^{-T}(D_k+Y_k^T{H}_0{Y}_k)R_k^{-1}& -R_k^{-T}\\ -R_k^{-1}& 0\end{array}\right]$ The direct Hessian approximation can be found by applying the Sherman-Morrison-Woodbury identity to the inverse Hessian:

$B_k=B_0+J_k{N}_k^{-1}{J}_k^T,J_k=\left[\begin{array}{cc}{B}_0{S}_k& Y_k\end{array}\right],N_k=\left[\begin{array}{cc}{S}^T{B}_0{S}_k& L_k\\ L_k^T& -D_k\end{array}\right]$

SR1

The SR1 (Symmetric Rank-1) compact representation was first proposed in. Using the definitions of $D_k,L_k$ and $R_k$ from above, the inverse Hessian formula is given by

$H_k=H_0+U_k{M}_k^{-1}{U}_k^T,U_k=S_k-H_0{Y}_k,M_k=R_k+R_k^T-D_k-Y_k^T{H}_0{Y}_k$

The direct Hessian is obtained by the Sherman-Morrison-Woodbury identity and has the form

$B_k=B_0+J_k{N}_k^{-1}{J}_k^T,J_k=Y_k-B_0{S}_k,N_k=D_k+L_k+L_k^T-S_k^T{B}_0{S}_k$

MSS

The multipoint symmetric secant (MSS) method is a method that aims to satisfy multiple secant equations. The recursive update formula was originally developed by Burdakov. The compact representation for the direct Hessian was derived in

$B_k=B_0+J_k{N}_k^{-1}{J}_k^T,J_k=\left[\begin{array}{cc}{S}_k& Y_k-B_0{S}_k\end{array}\right],N_k={\left[\begin{array}{cc}{W}_k(S_k^T{B}_0{S}_k-(R_k-D_k+R_k^T))W_k& W_k\\ W_k& 0\end{array}\right]}^{-1},W_k=(S_k^T{S}_k{)}^{-1}$

Another equivalent compact representation for the MSS matrix is derived by rewriting $J_k$ in terms of $J_k=\left[\begin{array}{cc}{S}_k& B_0{Y}_k\end{array}\right]$. The inverse representation can be obtained by application for the Sherman-Morrison-Woodbury identity.

DFP

Since the DFP (Davidon Fletcher Powell) update is the dual of the BFGS formula (i.e., swapping $H_k\leftrightarrow B_k$, $H_0\leftrightarrow B_0$ and $y_k\leftrightarrow s_k$ in the BFGS update), the compact representation for DFP can be immediately obtained from the one for BFGS.

PSB

The PSB (Powell-Symmetric-Broyden) compact representation was developed for the direct Hessian approximation. It is equivalent to substituting $C_k=S_k$ in (Template:EquationNote)

$B_k=B_0+J_k{N}_k^{-1}{J}_k^T,J_k=\left[\begin{array}{cc}{S}_k& Y_k-B_0{S}_k\end{array}\right],N_k=\left[\begin{array}{cc}0& R_k^{\text{SS}}\\ (R_k^{\text{SS}}{)}^T& R_k+R_k^T-(D_k+S_k^T{B}_0{S}_k)\end{array}\right]$

Structured BFGS

For structured optimization problems in which the objective function can be decomposed into two parts $f(x)=\hat{k}(x)+\hat{u}(x)$, where the gradients and Hessian of $\hat{k}(x)$ are known but only the gradient of $\hat{u}(x)$ is known, structured BFGS formulas exist. The compact representation of these methods has the general form of (Template:EquationNote), with specific $J_k$ and $N_k$.

Reduced BFGS

The reduced compact representation (RCR) of BFGS is for linear equality constrained optimization $\text{ minimize }f(x)\text{ subject to: }Ax=b$, where $A$ is underdetermined. In addition to the matrices $S_k,Y_k$ the RCR also stores the projections of the $y_i$'s onto the nullspace of $A$

$$Z_k=\left[\begin{array}{ccc}{z}_0& z_1& \cdots z_{k-1}\end{array}\right],z_i=P{y}_i,P=I-A(A^{T}A{)}^{-1}{A}^T,0\le i\le k-1$$

For $B_k$ the compact representation of the BFGS matrix (with a multiple of the identity $B_0$) the (1,1) block of the inverse KKT matrix has the compact representation

$K_k=\left[\begin{array}{cc}{B}_k& A^T\\ A& 0\end{array}\right],B_0=\frac{1}{{\gamma }_k}I,H_0={\gamma }_{k}I,{\gamma }_k>0$

$(K_k^{-1}{)}_{11}=H_0+U_k{M}_k^{-1}{U}_k^T,U_k=\left[\begin{array}{ccc}{A}^T& S_k& Z_k\end{array}\right],M_k=\left[\begin{array}{cc}-A{A}^T/{\gamma }_k& \\ & G_k\end{array}\right],G_k={\left[\begin{array}{cc}{R}_k^{-T}(D_k+Y_k^T{H}_0{Y}_k)R_k^{-1}& -H_0{R}_k^{-T}\\ -H_0{R}_k^{-1}& 0\end{array}\right]}^{-1}$

Limited Memory

Pattern in a limited-memory updating strategy. With a memory parameter of $m=7$, the first $k\le m$ iterations fill the matrix (e.g., an upper triangular for the compact representation, $R_k=\text{triu}(S_k^T{Y}_k)$). For $k>m$ the limited-memory techniques discards the oldest information and add a new column to the end.

The most common use of the compact representations is for the limited-memory setting where $m\ll n$ denotes the memory parameter, with typical values around $m\in [5,12]$ (see e.g.,). Then, instead of storing the history of all vectors one limits this to the $m$ most recent vectors $\{(s_i,y_i{\}}_{i=k-m}^{k-1}$ and possibly $\{v_i{\}}_{i=k-m}^{k-1}$ or $\{c_i{\}}_{i=k-m}^{k-1}$. Further, typically the initialization is chosen as an adaptive multiple of the identity $H_k^{(0)}={\gamma }_{k}I$, with ${\gamma }_k=y_{k-1}^T{s}_{k-1}/y_{k-1}^T{y}_{k-1}$ and $B_k^{(0)}=\frac{1}{{\gamma }_k}I$. Limited-memory methods are frequently used for large-scale problems with many variables (i.e., $n$ can be large), in which the limited-memory matrices $S_k\in {ℝ}^{n\times m}$ and $Y_k\in {ℝ}^{n\times m}$ (and possibly $V_k,C_k$) are tall and very skinny: $S_k=\left[\begin{array}{ccc}{s}_{k-l-1}& \dots & s_{k-1}\end{array}\right]$ and $Y_k=\left[\begin{array}{ccc}{y}_{k-l-1}& \dots & y_{k-1}\end{array}\right]$.

Implementations

Open source implementations include:

• ACM TOMS algorithm 1030 implements a L-SR1 solver
• R's optim general-purpose optimizer routine uses the L-BFGS-B method.
• SciPy's optimization module's minimize method also includes an option to use L-BFGS-B.
• IPOPT with first order information

Non open source implementations include:

• Artelys Knitro nonlinear programming (NLP) solvers use compact quasi-Newton matrices
• L-BFGS-B (ACM TOMS algorithm 778)