Catenoid

A catenoid

A catenoid obtained from the rotation of a catenary

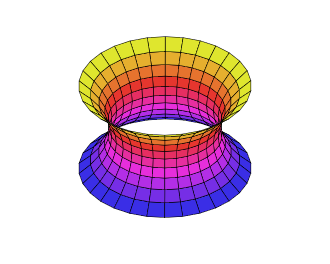
In geometry, a catenoid is a type of surface, arising by rotating a catenary curve about an axis (a surface of revolution). It is a minimal surface, meaning that it occupies the least area when bounded by a closed space. It was formally described in 1744 by the mathematician Leonhard Euler.

Soap film attached to twin circular rings will take the shape of a catenoid. Because they are members of the same associate family of surfaces, a catenoid can be bent into a portion of a helicoid, and vice versa.

Geometry

The catenoid was the first non-trivial minimal surface in 3-dimensional Euclidean space to be discovered apart from the plane. The catenoid is obtained by rotating a catenary about its directrix. It was found and proved to be minimal by Leonhard Euler in 1744.

Early work on the subject was published also by Jean Baptiste Meusnier.Template:Rp There are only two minimal surfaces of revolution (surfaces of revolution which are also minimal surfaces): the plane and the catenoid.

The catenoid may be defined by the following parametric equations: $$\begin{array}{cc}x& =c\cosh \frac{v}{c}\cos u\\ y& =c\cosh \frac{v}{c}\sin u\\ z& =v\end{array}$$ where $u\in [-\pi ,\pi )$ and $v\in ℝ$ and $c$ is a non-zero real constant.

In cylindrical coordinates: $$\rho =c\cosh \frac{z}{c},$$ where $c$ is a real constant.

A physical model of a catenoid can be formed by dipping two circular rings into a soap solution and slowly drawing the circles apart.

The catenoid may be also defined approximately by the stretched grid method as a facet 3D model.

Helicoid transformation

Deformation of a right-handed helicoid into a left-handed one and back again via a catenoid

Because they are members of the same associate family of surfaces, one can bend a catenoid into a portion of a helicoid without stretching. In other words, one can make a (mostly) continuous and isometric deformation of a catenoid to a portion of the helicoid such that every member of the deformation family is minimal (having a mean curvature of zero). A parametrization of such a deformation is given by the system $$\begin{array}{cc}x(u,v)& =\sin \theta \cosh v\cos u+\cos \theta \sinh v\sin u\\ y(u,v)& =\sin \theta \cosh v\sin u-\cos \theta \sinh v\cos u\\ z(u,v)& =v\sin \theta +u\cos \theta \end{array}$$ for $(u,v)\in (-\pi ,\pi ]\times (-\mathrm{\infty },\mathrm{\infty })$, with deformation parameter $-\pi <\theta \le \pi$, where:

• $\theta =\pi$ corresponds to a right-handed helicoid,
• $\theta =\pm \pi /2$ corresponds to a catenoid, and
• $\theta =0$ corresponds to a left-handed helicoid.

Further reading

• Template:Cite book

External links

• Template:Springer
• Catenoid – WebGL model
• Euler's text describing the catenoid at Carnegie Mellon University
• Calculating the surface area of a Catenoid
• Minimal Surface of Revolution