Order-4 octahedral honeycomb
| Order-4 octahedral honeycomb | |
|---|---|
 Perspective projection view within Poincaré disk model | |
| Type | Hyperbolic regular honeycomb Paracompact uniform honeycomb |
| Schläfli symbols | {3,4,4} {3,41,1} |
| Coxeter diagrams | Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD |
| Cells | {3,4} |
| Faces | triangle {3} |
| Edge figure | square {4} |
| Vertex figure | square tiling, {4,4} |
| Dual | Square tiling honeycomb, {4,4,3} |
| Coxeter groups | , [3,4,4] , [3,41,1] |
| Properties | Regular |
The order-4 octahedral honeycomb is a regular paracompact honeycomb in hyperbolic 3-space. It is paracompact because it has infinite vertex figures, with all vertices as ideal points at infinity. Given by Schläfli symbol {3,4,4}, it has four ideal octahedra around each edge, and infinite octahedra around each vertex in a square tiling vertex figure.[1]
Symmetry
A half symmetry construction, [3,4,4,1+], exists as {3,41,1}, with two alternating types (colors) of octahedral cells: Template:CDD ↔ Template:CDD.
A second half symmetry is [3,4,1+,4]: Template:CDD ↔ Template:CDD.
A higher index sub-symmetry, [3,4,4*], which is index 8, exists with a pyramidal fundamental domain, [((3,∞,3)),((3,∞,3))]: Template:CDD.
This honeycomb contains Template:CDD and Template:CDD that tile 2-hypercycle surfaces, which are similar to the paracompact infinite-order triangular tilings Template:CDD and Template:CDD, respectively:
Related polytopes and honeycombs
The order-4 octahedral honeycomb is a regular hyperbolic honeycomb in 3-space, and is one of eleven regular paracompact honeycombs. Template:Regular paracompact H3 honeycombs
There are fifteen uniform honeycombs in the [3,4,4] Coxeter group family, including this regular form. Template:443 family
It is a part of a sequence of honeycombs with a square tiling vertex figure: Template:Square tiling vertex figure tessellations
It a part of a sequence of regular polychora and honeycombs with octahedral cells: Template:Octahedral cell tessellations
Rectified order-4 octahedral honeycomb
| Rectified order-4 octahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | r{3,4,4} or t1{3,4,4} |
| Coxeter diagrams | Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD |
| Cells | r{4,3} {4,4} |
| Faces | triangle {3} square {4} |
| Vertex figure |  square prism |
| Coxeter groups | , [3,4,4] , [3,41,1] |
| Properties | Vertex-transitive, edge-transitive |
The rectified order-4 octahedral honeycomb, t1{3,4,4}, Template:CDD has cuboctahedron and square tiling facets, with a square prism vertex figure.
Truncated order-4 octahedral honeycomb
| Truncated order-4 octahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | t{3,4,4} or t0,1{3,4,4} |
| Coxeter diagrams | Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD |
| Cells | t{3,4} {4,4} |
| Faces | square {4} hexagon {6} |
| Vertex figure | 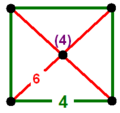 square pyramid |
| Coxeter groups | , [3,4,4] , [3,41,1] |
| Properties | Vertex-transitive |
The truncated order-4 octahedral honeycomb, t0,1{3,4,4}, Template:CDD has truncated octahedron and square tiling facets, with a square pyramid vertex figure.
Bitruncated order-4 octahedral honeycomb
The bitruncated order-4 octahedral honeycomb is the same as the bitruncated square tiling honeycomb.
Cantellated order-4 octahedral honeycomb
| Cantellated order-4 octahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | rr{3,4,4} or t0,2{3,4,4} s2{3,4,4} |
| Coxeter diagrams | Template:CDD Template:CDD Template:CDD ↔ Template:CDD |
| Cells | rr{3,4} {}x4 r{4,4} |
| Faces | triangle {3} square {4} |
| Vertex figure |  wedge |
| Coxeter groups | , [3,4,4] , [3,41,1] |
| Properties | Vertex-transitive |
The cantellated order-4 octahedral honeycomb, t0,2{3,4,4}, Template:CDD has rhombicuboctahedron, cube, and square tiling facets, with a wedge vertex figure.
Cantitruncated order-4 octahedral honeycomb
| Cantitruncated order-4 octahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | tr{3,4,4} or t0,1,2{3,4,4} |
| Coxeter diagrams | Template:CDD Template:CDD ↔ Template:CDD |
| Cells | tr{3,4} {}x{4} t{4,4} |
| Faces | square {4} hexagon {6} octagon {8} |
| Vertex figure | 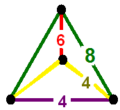 mirrored sphenoid |
| Coxeter groups | , [3,4,4] , [3,41,1] |
| Properties | Vertex-transitive |
The cantitruncated order-4 octahedral honeycomb, t0,1,2{3,4,4}, Template:CDD has truncated cuboctahedron, cube, and truncated square tiling facets, with a mirrored sphenoid vertex figure.
Runcinated order-4 octahedral honeycomb
The runcinated order-4 octahedral honeycomb is the same as the runcinated square tiling honeycomb.
Runcitruncated order-4 octahedral honeycomb
| Runcitruncated order-4 octahedral honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | t0,1,3{3,4,4} |
| Coxeter diagrams | Template:CDD Template:CDD ↔ Template:CDD |
| Cells | t{3,4} {6}x{} rr{4,4} |
| Faces | square {4} hexagon {6} octagon {8} |
| Vertex figure |  square pyramid |
| Coxeter groups | , [3,4,4] |
| Properties | Vertex-transitive |
The runcitruncated order-4 octahedral honeycomb, t0,1,3{3,4,4}, Template:CDD has truncated octahedron, hexagonal prism, and square tiling facets, with a square pyramid vertex figure.
Runcicantellated order-4 octahedral honeycomb
The runcicantellated order-4 octahedral honeycomb is the same as the runcitruncated square tiling honeycomb.
Omnitruncated order-4 octahedral honeycomb
The omnitruncated order-4 octahedral honeycomb is the same as the omnitruncated square tiling honeycomb.
Snub order-4 octahedral honeycomb
| Snub order-4 octahedral honeycomb | |
|---|---|
| Type | Paracompact scaliform honeycomb |
| Schläfli symbols | s{3,4,4} |
| Coxeter diagrams | Template:CDD Template:CDD ↔ Template:CDD Template:CDD Template:CDD ↔ Template:CDD Template:CDD ↔ Template:CDD |
| Cells | square tiling icosahedron square pyramid |
| Faces | triangle {3} square {4} |
| Vertex figure | |
| Coxeter groups | [4,4,3+] [41,1,3+] [(4,4,(3,3)+)] |
| Properties | Vertex-transitive |
The snub order-4 octahedral honeycomb, s{3,4,4}, has Coxeter diagram Template:CDD. It is a scaliform honeycomb, with square pyramid, square tiling, and icosahedron facets.
See also
- Convex uniform honeycombs in hyperbolic space
- Regular tessellations of hyperbolic 3-space
- Paracompact uniform honeycombs
References
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. Template:Isbn. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, Template:LCCN, Template:Isbn (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
- Jeffrey R. Weeks The Shape of Space, 2nd edition Template:Isbn (Chapter 16-17: Geometries on Three-manifolds I, II)
- Norman Johnson Uniform Polytopes, Manuscript
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- N.W. Johnson: Geometries and Transformations, (2015) Chapter 13: Hyperbolic Coxeter groups
- Norman W. Johnson and Asia Ivic Weiss Quadratic Integers and Coxeter Groups PDF Can. J. Math. Vol. 51 (6), 1999 pp. 1307–1336
- ↑ Coxeter The Beauty of Geometry, 1999, Chapter 10, Table III





