Hunt–Szymanski algorithm

In computer science, the Hunt–Szymanski algorithm, also known as Hunt–McIlroy algorithm, is a solution to the longest common subsequence problem. It was one of the first non-heuristic algorithms used in diff which compares a pair of files each represented as a sequence of lines. To this day, variations of this algorithm are found in incremental version control systems, wiki engines, and molecular phylogenetics research software.

The worst-case complexity for this algorithm is Template:Math, but in practice Template:Math is rather expected.

History

The algorithm was proposed by Harold S. Stone as a generalization of a special case solved by Thomas G. Szymanski. James W. Hunt refined the idea, implemented the first version of the candidate-listing algorithm used by diff and embedded it into an older framework of Douglas McIlroy.

The description of the algorithm appeared as a technical report by Hunt and McIlroy in 1976. The following year, a variant of the algorithm was finally published in a joint paper by Hunt and Szymanski.

Algorithm

The Hunt–Szymanski algorithm is a modification to a basic solution for the longest common subsequence problem which has complexity Template:Math. The solution is modified so that there are lower time and space requirements for the algorithm when it is working with typical inputs.

Basic longest common subsequence solution

Algorithm

Let Template:Math be the Template:Mathth element of the first sequence.

Let Template:Math be the Template:Mathth element of the second sequence.

Let Template:Math be the length of the longest common subsequence for the first Template:Math elements of Template:Math and the first Template:Math elements Template:Math.

$P_{ij}=\{\begin{array}{cc}0& \text{ if }i=0\text{ or }j=0\\ 1+P_{i-1,j-1}& \text{ if }{A}_i=B_j\\ \max (P_{i-1,j},P_{i,j-1})& \text{ if }{A}_i\ne B_j\end{array}$

Example

A table showing the recursive steps that the basic longest common subsequence algorithm takes

Consider the sequences Template:Math and Template:Math.

Template:Math contains three elements:

$\begin{array}{c}{A}_1=a\\ A_2=b\\ A_3=c\end{array}$

Template:Math contains three elements:

$\begin{array}{c}{B}_1=a\\ B_2=c\\ B_3=b\end{array}$

The steps that the above algorithm would perform to determine the length of the longest common subsequence for both sequences are shown in the diagram. The algorithm correctly reports that the longest common subsequence of the two sequences is two elements long.

Complexity

The above algorithm has worst-case time and space complexities of Template:Math (see big O notation), where Template:Math is the number of elements in sequence Template:Math and Template:Math is the number of elements in sequence Template:Math. The Hunt–Szymanski algorithm modifies this algorithm to have a worst-case time complexity of Template:Math and space complexity of Template:Math, though it regularly beats the worst case with typical inputs.

Essential matches

Template:Math-candidates

The Hunt–Szymanski algorithm only considers what the authors call essential matches, or Template:Math-candidates. Template:Math-candidates are pairs of indices Template:Math such that:

$A_i=B_j$

$P_{ij}>max(P_{i-1,j},P_{i,j-1})$

The second point implies two properties of Template:Math-candidates:

• There is a common subsequence of length Template:Math in the first Template:Math elements of sequence Template:Math and the first Template:Math elements of sequence Template:Math.
• There are no common subsequences of length Template:Math for any fewer than Template:Math elements of sequence Template:Math or Template:Math elements of sequence Template:Math.

Connecting Template:Math-candidates

A diagram that shows how using Template:Math-candidates reduces the amount of time and space needed to find the longest common subsequence of two sequences.

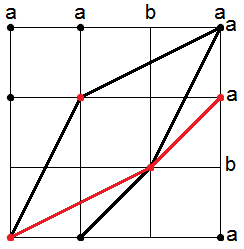
To create the longest common subsequence from a collection of Template:Math-candidates, a grid with each sequence's contents on each axis is created. The Template:Math-candidates are marked on the grid. A common subsequence can be created by joining marked coordinates of the grid such that any increase in Template:Math is accompanied by an increase in Template:Math.

This is illustrated in the adjacent diagram.

Black dots represent candidates that would have to be considered by the simple algorithm and the black lines are connections that create common subsequences of length 3.

Red dots represent Template:Math-candidates that are considered by the Hunt–Szymanski algorithm and the red line is the connection that creates a common subsequence of length 3.

See also

• Levenshtein distance
• Longest common subsequence problem
• Wagner–Fischer algorithm