File:Steiner chain animation-50dpi.gif
From testwiki
Jump to navigation
Jump to search
Steiner_chain_animation-50dpi.gif (250 × 251 pixels, file size: 1.35 MB, MIME type: image/gif, looped, 126 frames)
This file is from Wikimedia Commons and may be used by other projects. The description on its file description page there is shown below.
Summary
| DescriptionSteiner chain animation-50dpi.gif |
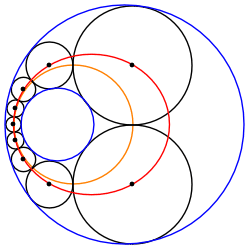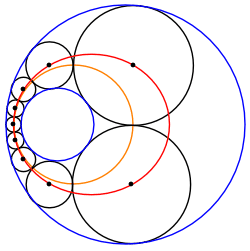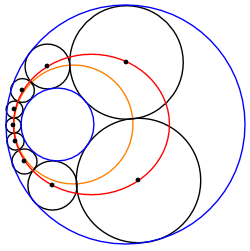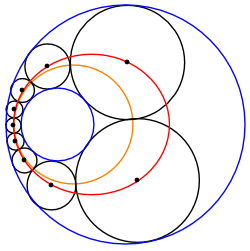
English: Animation of a Steiner chain of 9 circles, showing that the locus of the position of the circles' centres is an ellipse (in red), and that the locus of the contact points between the circles is a circle itself (in orange) |
| Date | |
| Source | https://twitter.com/j_bertolotti/status/1039543306433249280 |
| Author | Jacopo Bertolotti |
| Permission (Reusing this file) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 11.0 code
n = 9;
\[Theta] = \[Pi]/n;
\[CapitalDelta]\[Theta] = (2 \[Pi])/n;
R = 0.2;
\[Rho] = R/(1 + 1/Sin[\[Theta]]);
r = \[Rho] (1/Sin[\[Theta]] - 1);
center = {.3, 0};
plots = Reap[For[start = 0, start <= 2 \[Pi], start = start + 0.05,
CandR =
Table[{center[[1]] + (\[Rho] + r) Cos[i],
center[[2]] + (\[Rho] + r) Sin[i], \[Rho]}, {i, start,
start + (n -
1)*\[CapitalDelta]\[Theta], \[CapitalDelta]\[Theta]}];
createcoord[{x_, y_,
z_}] := {(x )/(x^2 + y^2 - z^2), (y)/(x^2 + y^2 - z^2),
z/(x^2 + y^2 - z^2)};
innerc = createcoord[Flatten[{center, r}]];
outherc = createcoord[Flatten[{center, R}]];
ellipseCenter = {(outherc[[1]] + innerc[[1]])/2, 0};
ellipseA =
Abs[createcoord[{center[[1]] + \[Rho] + r, 0, \[Rho]}][[1]] -
ellipseCenter[[1]]];
ellipseC = (outherc[[1]] - innerc[[1]])/2;
ellipseB = Sqrt[ellipseA^2 - ellipseC^2];
tmp = Map[createcoord, CandR];
p1 = {x, y} /.
Solve[{(x - tmp[[1, 1]])^2 + (y - tmp[[1, 2]])^2 ==
tmp[[1,
3]]^2 && (x - tmp[[2, 1]])^2 + (y - tmp[[2, 2]])^2 ==
tmp[[2, 3]]^2}, {x, y}][[1]];
p2 = {x, y} /.
Solve[{(x - tmp[[3, 1]])^2 + (y - tmp[[3, 2]])^2 ==
tmp[[3,
3]]^2 && (x - tmp[[2, 1]])^2 + (y - tmp[[2, 2]])^2 ==
tmp[[2, 3]]^2}, {x, y}][[1]];
p3 = {x, y} /.
Solve[{(x - tmp[[3, 1]])^2 + (y - tmp[[3, 2]])^2 ==
tmp[[3,
3]]^2 && (x - tmp[[4, 1]])^2 + (y - tmp[[4, 2]])^2 ==
tmp[[4, 3]]^2}, {x, y}][[1]];
c =
Abs[{xc, yc, rc} /.
Solve[((#1 - xc)^2 + (#2 - yc)^2 == rc^2) & @@@ {p1, p2,
p3}, {xc, yc, rc}][[1]] ];
Sow@Show[
Graphics[{Orange, Thick,
Evaluate[Circle[{c[[1]], c[[2]]}, c[[3]]] ]}],
Graphics[{Black, Thick,
Circle[{#1, #2}, #3] & @@@ Map[createcoord, CandR] }],
Graphics[{Blue, Thick,
Circle[{#1, #2}, #3] & @@@ {innerc, outherc} }],
Graphics[{Red, Thick,
Circle[ellipseCenter, {ellipseA, ellipseB}]}],
Graphics[{PointSize[0.02],
Point[Map[createcoord, CandR][[All, 1 ;; 2]]] }]
];
];][[2, 1]];
ListAnimate[plots]
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
| This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. | |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
This file, which was originally posted to
https://twitter.com/j_bertolotti/status/1039543306433249280, was reviewed on 19 October 2018 by reviewer Ronhjones, who confirmed that it was available there under the stated license on that date.
|
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
some value
11 September 2018
image/gif
1,410,765 B
251 pixel
250 pixel
09fe40aeaa7cd25b2577f441581d8527522e4761
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 09:29, 12 September 2018 | 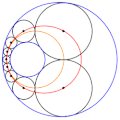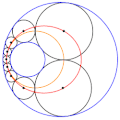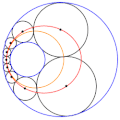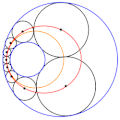 | 250 × 251 (1.35 MB) | wikimediacommons>Berto | User created page with UploadWizard |
File usage
The following page uses this file: