File:Illustration CRPS.png
From testwiki
Jump to navigation
Jump to search
Illustration_CRPS.png (547 × 432 pixels, file size: 18 KB, MIME type: image/png)
This file is from Wikimedia Commons and may be used by other projects. The description on its file description page there is shown below.
Summary
| DescriptionIllustration CRPS.png |
English: Illustration of the continous ranked probability score (CRPS). Given a sample y and a predicted cumulative distribution F, the CRPS is given by computing the difference between the curves at each point x of the support, squaring it and integrating it over the whole support.
Deutsch: Illustration des kontinuierlichen Rang-Wahrscheinlichkeits-Scores (CRPS). Gegeben ist eine Stichprobe y und eine vorhergesagte kumulative Verteilung F. Der CRPS wird berechnet, indem man die Differenz zwischen den Kurven an jedem Punkt x des Trägers berechnet, diese Differenz quadriert und über den gesamten Träger integriert. |
| Date | |
| Source | Own work |
| Author | Biggerj1 |
import matplotlib.pyplot as plt
import numpy as np
# Define the step function
def step_function(x):
return 0 if x < 0 else 1
# Define the sigmoid function
def sigmoid_function(x):
return 1 / (1 + np.exp(-x))
# Generate x values
x_high_res = np.linspace(-10, 10, 1000) # High resolution for the functions
x_low_res = np.linspace(-10, 10, 71) # Low resolution for the bars
# Calculate y values for both functions
y_step = [step_function(i) for i in x_high_res]
y_sigmoid = [sigmoid_function(i) for i in x_high_res]
# Plot both functions
plt.plot(x_high_res, y_step, label=r'$\mathbb{1}_{x>y}$')
plt.plot(x_high_res, y_sigmoid, label='F')
# Create a series of vertical bars to represent the area between the two functions
for i in range(len(x_low_res) - 1):
bar_height = abs(sigmoid_function(x_low_res[i]) - step_function(x_low_res[i]))
bar_width = x_low_res[i+1]-x_low_res[i] if i != len(x_low_res) - 2 else x_low_res[-1]-x_low_res[-2]
plt.bar(x_low_res[i], bar_height, bottom=min(step_function(x_low_res[i]), sigmoid_function(x_low_res[i])), width=bar_width, color='grey', align='edge', alpha=0.5)
# Add an annotation for the grey area
plt.annotate('CRPS', xy=(0.75, 0.75), xytext=(-3, 0.7),
arrowprops=dict(facecolor='black', shrink=0.05))
# Add labels and title
plt.xlabel('x')
#plt.title('Step Function vs Sigmoid Function')
plt.legend()
# Display the plot
plt.show()
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
Captions
Illustration of the continous ranked probability score (CRPS).
Items portrayed in this file
depicts
4 September 2023
image/png
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 21:00, 4 September 2023 | 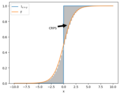 | 547 × 432 (18 KB) | wikimediacommons>Biggerj1 | Uploaded own work with UploadWizard |
File usage
The following page uses this file:
