File:Duration-bandwidth product.gif
Jump to navigation
Jump to search
No higher resolution available.
Duration-bandwidth_product.gif (800 × 261 pixels, file size: 2.93 MB, MIME type: image/gif, looped, 305 frames, 31 s)
Note: Due to technical limitations, thumbnails of high resolution GIF images such as this one will not be animated.
Summary
| Description |
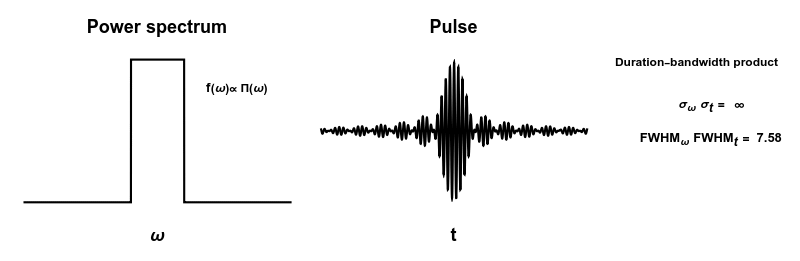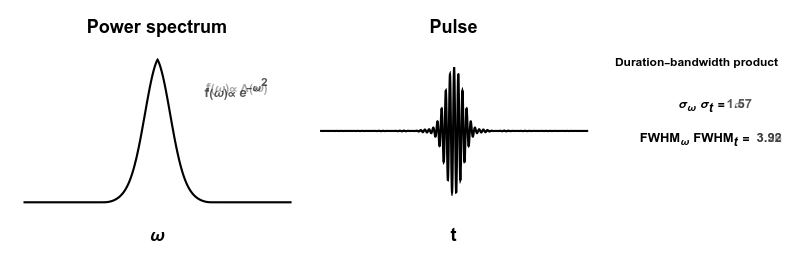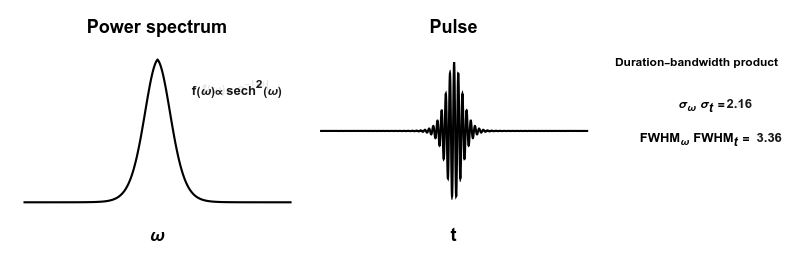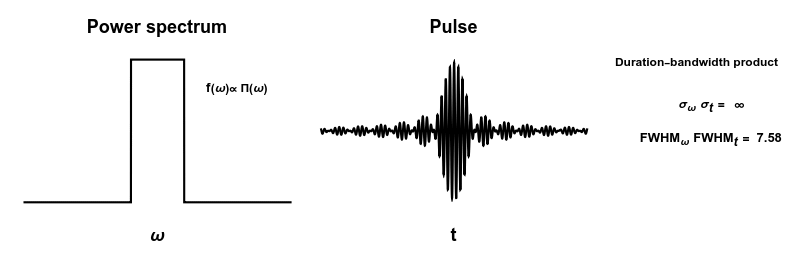
English: How short you can make a pulse depends on many frequencies you are using (bandwidth). But the "duration-bandwidth product" depends only on the shape of your power spectrum.
Interestingly, the question "which power spectrum will result in the shortest pulse" depends A LOT on how you decide to measure how wide things are. In particular using the standard deviation or the full-width half-maximum, give very different numbers in many cases. |
| Date | |
| Source | https://twitter.com/j_bertolotti/status/1362719916449742848 |
| Author | Jacopo Bertolotti |
| Permission (Reusing this file) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 12.0 code
labels = {"f(\[Omega])\[Proportional] \[CapitalPi](\[Omega])", "f(\[Omega])\[Proportional] \[CapitalLambda](\[Omega])", "f(\[Omega])\[Proportional] \!\(\*SuperscriptBox[\(e\), \\(-\*SuperscriptBox[\(\[Omega]\), \(2\)]\)]\)", "f(\[Omega])\[Proportional] \!\(\*SuperscriptBox[\(sech\), \\(2\)]\)(\[Omega])", "f(\[Omega])\[Proportional] \!\(\*SuperscriptBox[\(e\), \(-\(\(|\)\\(\[Omega]\)\(|\)\)\)]\)"};
frames = Table[
Table[
GraphicsRow[{
Plot[(1 - \[Tau]) f[[j]]^2 + \[Tau] f[[Mod[j + 1, 5, 1]]]^2, {\[Omega], -5, 5}, PlotRange -> {-0.1, 1.1}, Exclusions -> None, PlotStyle -> Black, Axes -> False, FrameLabel -> {{None, None}, {"\[Omega]", "Power spectrum"}}, Frame -> True, FrameStyle -> Directive[White, FontColor -> Black], LabelStyle -> {FontSize -> 14, Bold}, FrameTicks -> None, Epilog -> {Opacity[1 - \[Tau]], Text[Style[labels[[j]], Black, Bold], {3, 0.8}], Opacity[\[Tau]], Text[Style[labels[[Mod[j + 1, 5, 1]]], Black, Bold], {3, 0.8}]}
]
,
Plot[(1 - \[Tau]) p[[j]]*Cos[\[Omega]0 t] + \[Tau] p[[Mod[j + 1, 5, 1]]]*Cos[\[Omega]0 t], {t, -20, 20}, PlotStyle -> Black, PlotRange -> {-1, 1}, Axes -> False, FrameLabel -> {{None, None}, {"t", "Pulse"}}, Frame -> True, FrameStyle -> Directive[White, FontColor -> Black], LabelStyle -> {FontSize -> 14, Bold}, FrameTicks -> None]
,
Graphics[{Text[Style["Duration-bandwidth product", Black, Bold, FontSize -> 9], {0, 0.8}],
Text[Style["\!\(\*SubscriptBox[\(\[Sigma]\), \(\[Omega]\)]\) \!\(\\*SubscriptBox[\(\[Sigma]\), \(t\)]\) = ", Black, Bold, FontSize -> 10], {0.08, 0.3}], Opacity[1 - \[Tau]],
Text[Style[StringForm["``", NumberForm[\[Sigma]\[Omega][[j]]*\[Sigma]t[[j]] // N, {3, 2}]], Black, Bold, FontSize -> 10], {0.5, 0.32}], Opacity[\[Tau]],
Text[Style[StringForm["``", NumberForm[\[Sigma]\[Omega][[Mod[j + 1, 5, 1]]]*\[Sigma]t[[Mod[j + 1, 5, 1]]] // N, {3, 2}]], Black, Bold, FontSize -> 10], {0.5, 0.32}], Opacity[1],
Text[Style["\!\(\*SubscriptBox[\(FWHM\), \(\[Omega]\)]\) \\!\(\*SubscriptBox[\(FWHM\), \(t\)]\) = ", Black, Bold, FontSize -> 10], {0, -0.1}], Opacity[1 - \[Tau]],
Text[Style[StringForm["``", NumberForm[fwhm\[Omega][[j]]*fwhmt[[j]], {3, 2}]], Black, Bold, FontSize -> 10], {0.85, -0.08}], Opacity[\[Tau]],
Text[Style[StringForm["``", NumberForm[fwhm\[Omega][[Mod[j + 1, 5, 1]]]*fwhmt[[Mod[j + 1, 5, 1]]], {3, 2}]], Black, Bold, FontSize -> 10], {0.85, -0.08}]
}, PlotRange -> {{-1, 1}, {-1, 1}}]
}]
, {\[Tau]1, 0, 1, 0.02}]
, {j, 1, 5}];
ListAnimate[Join[Flatten@Table[{Table[frames[[j, 1]], {10}], frames[[j]]}, {j, 1, 5}] ]]
Licensing
I, the copyright holder of this work, hereby publish it under the following license:
 
|
This file is made available under the Creative Commons CC0 1.0 Universal Public Domain Dedication. |
| The person who associated a work with this deed has dedicated the work to the public domain by waiving all of their rights to the work worldwide under copyright law, including all related and neighboring rights, to the extent allowed by law. You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
|
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 18:30, 24 February 2021 | | 800 × 261 (2.93 MB) | wikimediacommons>Berto | Uploaded own work with UploadWizard |
File usage
The following page uses this file:
