Scorer's function

In mathematics, the Scorer's functions are special functions studied by Template:Harvtxt and denoted Gi(x) and Hi(x).
Hi(x) and -Gi(x) solve the equation
and are given by
The Scorer's functions can also be defined in terms of Airy functions:
It can also be seen, just from the integral forms, that the following relationship holds:
-
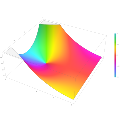
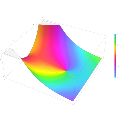
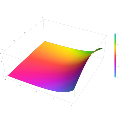
Plot of the Scorer function Gi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
-
Plot of the derivative of the Scorer function Hi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
-
Plot of the derivative of the Scorer function Gi'(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D
-
Plot of the Scorer function Hi(z) in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D