Maximum energy product

Historical trends in the maximum energy product of permanent magnets (MGOe units).

In magnetics, the maximum energy product is an important figure-of-merit for the strength of a permanent magnet material. It is often denoted Template:Math and is typically given in units of either Template:Math (kilojoules per cubic meter, in SI electromagnetism) or Template:Math (mega-gauss-oersted, in gaussian electromagnetism). 1 MGOe is equivalent to Template:Val.

During the 20th century, the maximum energy product of commercially available magnetic materials rose from around 1 MGOe (e.g. in KS Steel) to over 50 MGOe (in neodymium magnets). Other important permanent magnet properties include the remanence (Template:Math) and coercivity (Template:Math); these quantities are also determined from the saturation loop and are related to the maximum energy product, though not directly.

Definition and significance

Template:Math can be graphically defined as the area of the largest rectangle that can drawn in the second quadrant of the B-H loop.

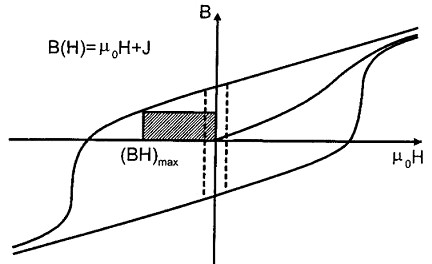
The maximum energy product is defined based on the magnetic hysteresis saturation loop (Template:Mvar-Template:Mvar curve), in the demagnetizing portion where the Template:Mvar and Template:Mvar fields are in opposition. It is defined as the maximal value of the product of Template:Mvar and Template:Mvar along this curve (actually, the maximum of the negative of the product, Template:Math, since they have opposing signs):

$(BH{)}_{\mathrm{m}\mathrm{a}\mathrm{x}}\equiv \max (-B\cdot H).$

Equivalently, it can be graphically defined as the area of the largest rectangle that can be drawn between the origin and the saturation demagnetization B-H curve (see figure).

The significance of Template:Math is that the volume of magnet necessary for any given application tends to be inversely proportional to Template:Math. This is illustrated by considering a simple magnetic circuit containing a permanent magnet of volume Template:Math and an air gap of volume Template:Math, connected to each other by a magnetic core. Suppose the goal is to reach a certain field strength Template:Math in the gap. In such a situation, the total magnetic energy in the gap (volume-integrated magnetic energy density) is directly equal to half the volume-integrated Template:Math in the magnet:

$E_{\mathrm{g}\mathrm{a}\mathrm{p}}=\frac{1}{2{\mu }_0}(B_{\mathrm{g}\mathrm{a}\mathrm{p}}{)}^2{\mathrm{V}\mathrm{o}\mathrm{l}}_{\mathrm{g}\mathrm{a}\mathrm{p}}=-\frac{1}{2}{B}_{\mathrm{m}\mathrm{a}\mathrm{g}}{H}_{\mathrm{m}\mathrm{a}\mathrm{g}}{\mathrm{V}\mathrm{o}\mathrm{l}}_{\mathrm{m}\mathrm{a}\mathrm{g}}=-E_{\mathrm{m}\mathrm{a}\mathrm{g}},$

thus in order to achieve the desired magnetic field in the gap, the required volume of magnet can be minimized by maximizing Template:Math in the magnet. By choosing a magnetic material with a high Template:Math, and also choosing the aspect ratio of the magnet so that its Template:Math is equal to Template:Math, the required volume of magnet to achieve a target flux density in the air gap is minimized. This expression assumes that the permeability in the core that is connecting the magnetic material to the air gap is infinite, so unlike the equation might imply, you cannot get arbitrarily large flux density in the air gap by decreasing the gap distance. A real core will eventually saturate.

See also

• Tetrataenite