Thin plate energy functional

The exact thin plate energy functional (TPEF) for a function $f(x,y)$ is

$\underset{y_0}{\overset{y_1}{\int }}\underset{x_0}{\overset{x_1}{\int }}({\kappa }_1^2+{\kappa }_2^2)\sqrt{g}dxdy$

where ${\kappa }_1$ and ${\kappa }_2$ are the principal curvatures of the surface mapping $f$ at the point $(x,y).$ This is the surface integral of ${\kappa }_1^2+{\kappa }_2^2,$ hence the $\sqrt{g}$ in the integrand.

Minimizing the exact thin plate energy functional would result in a system of non-linear equations. So in practice, an approximation that results in linear systems of equations is often used. The approximation is derived by assuming that the gradient of $f$ is 0. At any point where $f_x=f_y=0,$ the first fundamental form $g_{ij}$ of the surface mapping $f$ is the identity matrix and the second fundamental form $b_{ij}$ is

$\left(\begin{array}{cc}{f}_{xx}& f_{xy}\\ f_{xy}& f_{yy}\end{array}\right)$.

We can use the formula for mean curvature $H=b_{ij}{g}^{ij}/2$ to determine that $H=(f_{xx}+f_{yy})/2$ and the formula for Gaussian curvature $K=b/g$ (where $b$ and $g$ are the determinants of the second and first fundamental forms, respectively) to determine that $K=f_{xx}{f}_{yy}-(f_{xy}{)}^2.$ Since $H=(k_1+k_2)/2$ and $K=k_1{k}_2,$ the integrand of the exact TPEF equals $4H^2-2K.$ The expressions we just computed for the mean curvature and Gaussian curvature as functions of partial derivatives of $f$ show that the integrand of the exact TPEF is

$4H^2-2K=(f_{xx}+f_{yy}{)}^2-2(f_{xx}{f}_{yy}-f_{xy}^2)=f_{xx}^2+2f_{xy}^2+f_{yy}^2.$

So the approximate thin plate energy functional is

$J[f]=\underset{y_0}{\overset{y_1}{\int }}\underset{x_0}{\overset{x_1}{\int }}{f}_{xx}^2+2f_{xy}^2+f_{yy}^{2}dxdy.$

Rotational invariance

Rotating (x,y) by theta about z-axis to (X,Y)

Original surface with point (x,y)

Rotated surface with rotated point (X,Y)

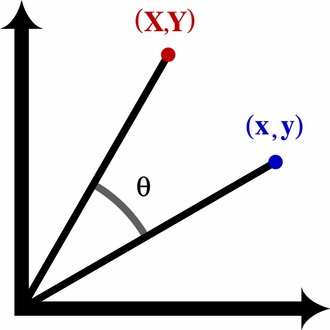
The TPEF is rotationally invariant. This means that if all the points of the surface $z(x,y)$ are rotated by an angle $\theta$ about the $z$-axis, the TPEF at each point $(x,y)$ of the surface equals the TPEF of the rotated surface at the rotated $(x,y).$ The formula for a rotation by an angle $\theta$ about the $z$-axis is

The fact that the $z$ value of the surface at $(x,y)$ equals the $z$ value of the rotated surface at the rotated $(x,y)$ is expressed mathematically by the equation

$Z(X,Y)=z(x,y)=(z\circ xy)(X,Y)$

where $xy$ is the inverse rotation, that is, $xy(X,Y)=R^{-1}(X,Y{)}^{\text{T}}=R^{\text{T}}(X,Y{)}^{\text{T}}.$ So $Z=z\circ xy$ and the chain rule implies

In equation (Template:EquationNote), $Z_0$ means $Z_X,$ $Z_1$ means $Z_Y,$ $z_0$ means $z_x,$ and $z_1$ means $z_y.$ Equation (Template:EquationNote) and all subsequent equations in this section use non-tensor summation convention, that is, sums are taken over repeated indices in a term even if both indices are subscripts. The chain rule is also needed to differentiate equation (Template:EquationNote) since $z_j$ is actually the composition $z_j\circ xy:$

$Z_{ik}=z_{jl}{R}_{kl}{R}_{ij}$.

Swapping the index names $j$ and $k$ yields

Expanding the sum for each pair $i,j$ yields

$\begin{array}{ccc}{Z}_{XX}& =& R_{00}^2{z}_{xx}+2R_{00}{R}_{01}{z}_{xy}+R_{01}^2{z}_{yy},\\ Z_{XY}& =& R_{00}{R}_{10}{z}_{xx}+(R_{00}{R}_{11}+R_{01}{R}_{10})z_{xy}+R_{01}{R}_{11}{z}_{yy},\\ Z_{YY}& =& R_{10}^2{z}_{xx}+2R_{10}{R}_{11}{z}_{xy}+R_{11}^2{z}_{yy}.\end{array}$

Computing the TPEF for the rotated surface yields

Inserting the coefficients of the rotation matrix $R$ from equation (Template:EquationNote) into the right-hand side of equation (Template:EquationNote) simplifies it to $z_{xx}^2+2z_{xy}^2+z_{yy}^2.$

Data fitting

The approximate thin plate energy functional can be used to fit B-spline surfaces to scattered 1D data on a 2D grid (for example, digital terrain model data). Call the grid points $(x_i,y_i)$ for $i=1\dots N$ (with $x_i\in [a,b]$ and $y_i\in [c,d]$) and the data values $z_i.$ In order to fit a uniform B-spline $f(x,y)$ to the data, the equation

(where $\lambda$ is the "smoothing parameter") is minimized. Larger values of $\lambda$ result in a smoother surface and smaller values result in a more accurate fit to the data. The following images illustrate the results of fitting a B-spline surface to some terrain data using this method.

• 
  Original terrain data
• 
  Fitted B-spline surface with large lambda and more smoothing
• 
  Fitted B-spline surface with smaller lambda and less smoothing

The thin plate smoothing spline also minimizes equation (Template:EquationNote), but it is much more expensive to compute than a B-spline and not as smooth (it is only $C^1$ at the "centers" and has unbounded second derivatives there).