Velocity filter

A velocity filter removes interfering signals by exploiting the difference between the travelling velocities of desired seismic waveform and undesired interfering signals.

Introduction

Template:Confusing In geophysical applications sensors are used to measure and record the seismic signals. Many filtering techniques are available in which one output waveform is produced with a higher signal-to-noise ratio than the individual sensor recordings. Velocity filters are designed to remove interfering signals by exploiting the difference between the travelling velocities of desired seismic waveform and undesired interfering signals. In contrast to the one dimensional output produced by multi-channel filtering, velocity filters produce a two-dimensional output.

Consider an array of Template:Mvar sensors that receive one desired and Template:Mvar undesired broadband interferences. Let the measurement of Template:Mvarth sensor be modeled by the expression:

where

• Template:Math;
• Template:Math;
• Template:Math are signals travelling across the array;
• Template:Math represents zero-mean white random noise at the Template:Mvarth sensor, uncorrelated from sensor to sensor.

The parameters Template:Math and Template:Math are amplitude gain and time delays of the signal Template:Math when received at the Template:Mvarth sensor.

Without loss of generality, we shall assume that Template:Math is the desired signal and Template:Math are the undesired interferences. Additionally we shall assume that Template:Math, and Template:Math. This essentially means that the data has been time shifted to align the desired seismic signal so that it appears on all sensors at the same time and balanced so that the desired signal appears with equal amplitudes. We assume that the signals are digitized prior to being recorded and that the length Template:Mvar of time sequences of recorded data is large enough for the complete delayed interfering waveforms to be included in the recorded data. In the discrete frequency domain, the Template:Mvarth trace can be expressed as:

where Template:Math is the sampling angular frequency.

Using matrix notation, (2) can be expressed in the form:

Velocity filtering

Frequency domain multichannel filters Template:Math can be applied to the data to produce one single output trace of the form:

In matrix form, the above expression can be written as:

where Template:Math is an Template:Math vector whose elements are the individual channel filters. That is,

By following the procedure discussed in Chen & Simaan (1990), an optimum filter vector F(k) can be designed to attenuate, in the least square sense, the undesired coherent interferences Template:Math while preserving the desired signal Template:Math in Template:Math. This filter can be shown to be of the form:

where Template:Mvar is an arbitrary Template:Math nonzero vector, Template:Math, Template:Mvar is the unit matrix, Template:Math is a submatrix of the matrix obtained by dropping all linearly dependent rows, and Template:Math is a lower triangular matrix satisfying:

$$[L(k)B_r(k)][L(k)B_r(k){]}^H=I$$ Template:NumBlk

The multichannel processing scheme described by equations 6 to 10 produces one dimensional output trace. A velocity filter, on the other hand, is a two-dimensional filter which produces a two-dimensional output record.

A two-dimensional record can be generated by a procedure which involves repeatedly applying multichannel optimum filters to a small number of overlapping subarrays of the input data,.

Fig. 1. A sliding subarray of multichannel filters

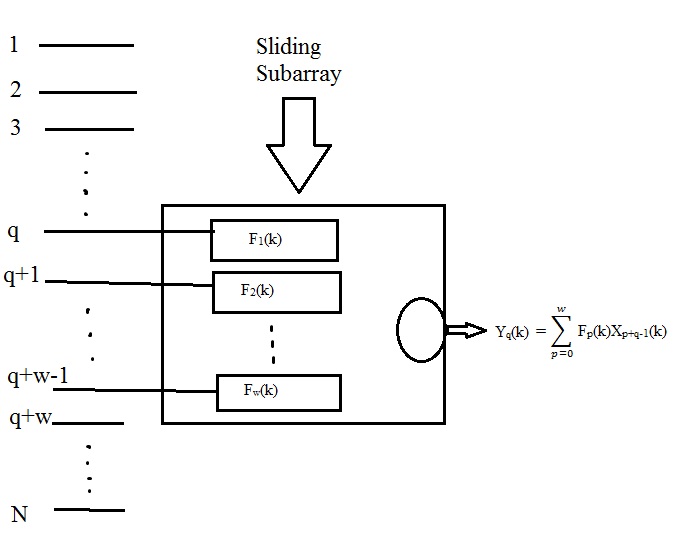
More specifically, consider a subarray of Template:Mvar channels, where Template:Math, which slides over the input data as shown in Fig. 1. For every subarray position an optimum multichannel filter based on (9) can be designed so that the undesired interferences are suppressed from its corresponding output trace. In designing this filter we use Template:Mvar instead of Template:Mvar in expression (9). Thus traces Template:Math of the input record produce the first trace of the output record, traces Template:Math of the input record produce the Template:Mvarth trace of the output record, and traces Template:Math of the input record produce the Template:Mathst trace, which is the last trace, of the output record. For a large Template:Mvar and small Template:Mvar, as is typically the case in geophysical data, the output record can be viewed as comparable in dimensions to the input record. Clearly for such a scheme to work effectively Template:Mvar must be as small as possible; while at the same time it must be large enough to provide the necessary attenuation of the undesired signals. Note that a maximum of Template:Math undesired interferences can be totally suppressed by such a scheme.