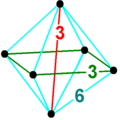
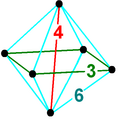
Octahedral pyramid
Template:Short description Template:Infobox 4-polytope
In 4-dimensional geometry, the octahedral pyramid is bounded by one octahedron on the base and 8 triangular pyramid cells which meet at the apex. Since an octahedron has a circumradius divided by edge length less than one,[1] the triangular pyramids can be made with regular faces (as regular tetrahedrons) by computing the appropriate height.
Having all regular cells, it is a Blind polytope. Two copies can be augmented to make an octahedral bipyramid which is also a Blind polytope.
Occurrences of the octahedral pyramid
The regular 16-cell has octahedral pyramids around every vertex, with the octahedron passing through the center of the 16-cell. Therefore placing two regular octahedral pyramids base to base constructs a 16-cell. The 16-cell tessellates 4-dimensional space as the 16-cell honeycomb.
Exactly 24 regular octahedral pyramids will fit together around a vertex in four-dimensional space (the apex of each pyramid). This construction yields a 24-cell with octahedral bounding cells, surrounding a central vertex with 24 edge-length long radii. The 4-dimensional content of a unit-edge-length 24-cell is 2, so the content of the regular octahedral pyramid is 1/12. The 24-cell tessellates 4-dimensional space as the 24-cell honeycomb.
The octahedral pyramid is the vertex figure for a truncated 5-orthoplex, Template:CDD.
The graph of the octahedral pyramid is the only possible minimal counterexample to Negami's conjecture, that the connected graphs with planar covers are themselves projective-planar.[2]
Example 4-dimensional coordinates, 6 points in first 3 coordinates for cube and 4th dimension for the apex.
Other polytopes
Cubic pyramid
The dual to the octahedral pyramid is a cubic pyramid, seen as a cubic base and 6 square pyramids meeting at an apex.
Example 4-dimensional coordinates, 8 points in first 3 coordinates for cube and 4th dimension for the apex. Template:-
Square-pyramidal pyramid

The square-pyramidal pyramid, Template:Nowrap, is a bisected octahedral pyramid. It has a square pyramid base, and 4 tetrahedrons along with another one more square pyramid meeting at the apex. It can also be seen in an edge-centered projection as a square bipyramid with four tetrahedra wrapped around the common edge. If the height of the two apexes are the same, it can be given a higher symmetry name Template:Nowrap joining an edge to a perpendicular square.[3]
The square-pyramidal pyramid can be distorted into a rectangular-pyramidal pyramid, Template:Nowrap or a rhombic-pyramidal pyramid, Template:Nowrap or other lower symmetry forms.
The square-pyramidal pyramid exists as a vertex figure in uniform polytopes of the form Template:CDD, including the bitruncated 5-orthoplex and bitruncated tesseractic honeycomb.
Example 4-dimensional coordinates, 2 coordinates for square, and axial points for pyramidal points.
References
External links
- Template:GlossaryForHyperspace
- Template:KlitzingPolytopes
- Richard Klitzing, Axial-Symmetrical Edge Facetings of Uniform Polyhedra
- ↑ Template:KlitzingPolytopes 1/sqrt(2) = 0.707107
- ↑ Template:Citation
- ↑ Template:KlitzingPolytopes