Sphere packing in a sphere

Sphere packing in a sphere is a three-dimensional packing problem with the objective of packing a given number of equal spheres inside a unit sphere. It is the three-dimensional equivalent of the circle packing in a circle problem in two dimensions.

Number of inner spheres	Maximum radius of inner spheres		Packing density	Optimality	Arrangement	Diagram
	Exact form	Approximate
1	$1$	1.0000	1	Trivially optimal.	Point
2	$\frac{1}{2}$	0.5000	0.25	Trivially optimal.	Line segment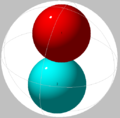
3	$2\sqrt{3}-3$	0.4641...	0.29988...	Trivially optimal.	Triangle
4	$\sqrt{6}-2$	0.4494...	0.36326...	Proven optimal.	Tetrahedron
5	$\sqrt{2}-1$	0.4142...	0.35533...	Proven optimal.	Trigonal bipyramid
6	$\sqrt{2}-1$	0.4142...	0.42640...	Proven optimal.	Octahedron
7	$\frac{1}{\frac{\sqrt{3}+2\cos \left(\frac{\pi }{18}\right)}{\sqrt{2+2\sqrt{3}\cos \left(\frac{\pi }{18}\right)}}+1}$	0.3859...	0.40231...	Proven optimal.	Capped octahedron
8	$\frac{1}{\sqrt{2+\frac{1}{\sqrt{2}}}+1}$	0.3780...	0.43217...	Proven optimal.	Square antiprism
9	$\frac{\sqrt{3}-1}{2}$	0.3660...	0.44134...	Proven optimal.	Tricapped trigonal prism
10		0.3530...	0.44005...	Proven optimal.
11	$\frac{\sqrt{5}-3}{2}+\sqrt{5-2\sqrt{5}}$	0.3445...	0.45003...	Proven optimal.	Diminished icosahedron
12	$\frac{\sqrt{5}-3}{2}+\sqrt{5-2\sqrt{5}}$	0.3445...	0.49095...	Proven optimal.	Icosahedron