Test functions for optimization
Template:Short description In applied mathematics, test functions, known as artificial landscapes, are useful to evaluate characteristics of optimization algorithms, such as convergence rate, precision, robustness and general performance.
Here some test functions are presented with the aim of giving an idea about the different situations that optimization algorithms have to face when coping with these kinds of problems. In the first part, some objective functions for single-objective optimization cases are presented. In the second part, test functions with their respective Pareto fronts for multi-objective optimization problems (MOP) are given.
The artificial landscapes presented herein for single-objective optimization problems are taken from Bäck,[1] Haupt et al.[2] and from Rody Oldenhuis software.[3] Given the number of problems (55 in total), just a few are presented here.
The test functions used to evaluate the algorithms for MOP were taken from Deb,[4] Binh et al.[5] and Binh.[6] The software developed by Deb can be downloaded,[7] which implements the NSGA-II procedure with GAs, or the program posted on Internet,[8] which implements the NSGA-II procedure with ES.
Just a general form of the equation, a plot of the objective function, boundaries of the object variables and the coordinates of global minima are given herein.
Test functions for single-objective optimization
| Name | Plot | Formula | Global minimum | Search domain |
|---|---|---|---|---|
| Rastrigin function | 
|
|
||
| Ackley function | 
|
|
||
| Sphere function | 
|
, | ||
| Rosenbrock function | 
|
, | ||
| Beale function | 
|
|
||
| Goldstein–Price function | 
|
|
||
| Booth function | 
|
|||
| Bukin function N.6 | 
|
, | ||
| Matyas function | 
|
|||
| Lévi function N.13 | 
|
|
||
| Griewank function | 
|
, where | , | |
| Himmelblau's function | 
|
|||
| Three-hump camel function | 
|
|||
| Easom function | 
|
|||
| Cross-in-tray function | 
|
|||
| Eggholder function[9][10] | 
|
|||
| Hölder table function | 
|
|||
| McCormick function | 
|
, | ||
| Schaffer function N. 2 | 
|
|||
| Schaffer function N. 4 | 
|
|||
| Styblinski–Tang function | 
|
, .. | ||
| Shekel function | 
|
or, similarly, |
, |
Test functions for constrained optimization
| Name | Plot | Formula | Global minimum | Search domain |
|---|---|---|---|---|
| Rosenbrock function constrained to a disk[11] | 
|
,
subjected to: |
, | |
| Mishra's Bird function - constrained[12][13] | 
|
,
subjected to: |
, | |
| Townsend function (modified)[14] | 
|
,
subjected to: where: Template:Math |
, | |
| Keane's bump functionTemplate:Anchor[15] | 
|
,
subjected to: , and |
Test functions for multi-objective optimization
| Name | Plot | Functions | Constraints | Search domain |
|---|---|---|---|---|
| Binh and Korn function:[5] | 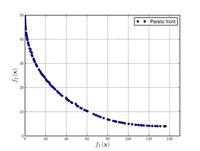
|
, | ||
| Chankong and Haimes function:[16] | 
|
|||
| Fonseca–Fleming function:[17] | 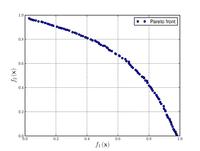
|
, | ||
| Test function 4:[6] | ![Test function 4.[6]](https://upload.wikimedia.org/wikipedia/commons/thumb/3/3c/Test_function_4_-_Binh.pdf/page1-200px-Test_function_4_-_Binh.pdf.jpg)
|
|||
| Kursawe function:[18] | 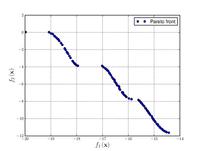
|
, . | ||
| Schaffer function N. 1:[19] | 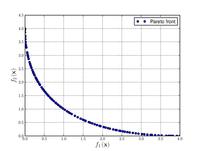
|
. Values of from to have been used successfully. Higher values of increase the difficulty of the problem. | ||
| Schaffer function N. 2: | 
|
. | ||
| Poloni's two objective function: | 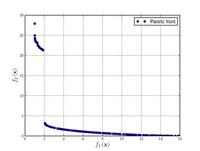
|
|
||
| Zitzler–Deb–Thiele's function N. 1:[20] | 
|
, . | ||
| Zitzler–Deb–Thiele's function N. 2:[20] | 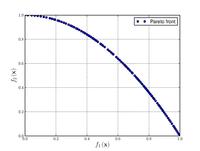
|
, . | ||
| Zitzler–Deb–Thiele's function N. 3:[20] | 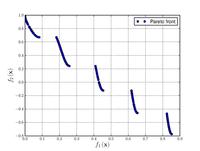
|
, . | ||
| Zitzler–Deb–Thiele's function N. 4:[20] | 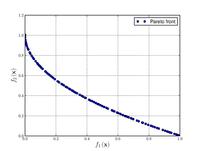
|
, , | ||
| Zitzler–Deb–Thiele's function N. 6:[20] | 
|
, . | ||
| Osyczka and Kundu function:[21] | 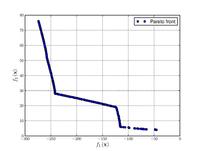
|
, , . | ||
| CTP1 function (2 variables):[4][22] | ![CTP1 function (2 variables).[4]](https://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/CTP1_function_%282_variables%29.pdf/page1-200px-CTP1_function_%282_variables%29.pdf.jpg)
|
. | ||
| Constr-Ex problem:[4] | ![Constr-Ex problem.[4]](https://upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Constr-Ex_problem.pdf/page1-200px-Constr-Ex_problem.pdf.jpg)
|
, | ||
| Viennet function: | 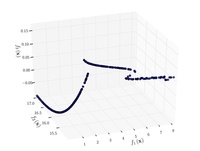
|
. |
References
- ↑ Template:Cite book
- ↑ Template:Cite book
- ↑ Template:Cite web
- ↑ 4.0 4.1 4.2 4.3 4.4 Deb, Kalyanmoy (2002) Multiobjective optimization using evolutionary algorithms (Repr. ed.). Chichester [u.a.]: Wiley. Template:Isbn.
- ↑ 5.0 5.1 Binh T. and Korn U. (1997) MOBES: A Multiobjective Evolution Strategy for Constrained Optimization Problems. In: Proceedings of the Third International Conference on Genetic Algorithms. Czech Republic. pp. 176–182
- ↑ 6.0 6.1 6.2 Binh T. (1999) A multiobjective evolutionary algorithm. The study cases. Technical report. Institute for Automation and Communication. Barleben, Germany
- ↑ Deb K. (2011) Software for multi-objective NSGA-II code in C. Available at URL: https://www.iitk.ac.in/kangal/codes.shtml
- ↑ Template:Cite web
- ↑ Template:Cite journal
- ↑ Vanaret C. (2015) Hybridization of interval methods and evolutionary algorithms for solving difficult optimization problems. PhD thesis. Ecole Nationale de l'Aviation Civile. Institut National Polytechnique de Toulouse, France.
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ Template:Cite journal
- ↑ Template:Cite web
- ↑ Template:Cite journal
- ↑ Template:Cite book
- ↑ Template:Cite journal
- ↑ F. Kursawe, “A variant of evolution strategies for vector optimization,” in PPSN I, Vol 496 Lect Notes in Comput Sc. Springer-Verlag, 1991, pp. 193–197.
- ↑ Template:Cite book
- ↑ 20.0 20.1 20.2 20.3 20.4 Template:Cite book
- ↑ Template:Cite journal
- ↑ Template:Cite book