Fraunhofer diffraction equation

Template:Short description Template:For Template:Broader In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.

The equation was named in honour of Joseph von Fraunhofer although he was not actually involved in the development of the theory.

This article gives the equation in various mathematical forms, and provides detailed calculations of the Fraunhofer diffraction pattern for several different forms of diffracting apertures, specially for normally incident monochromatic plane wave. A qualitative discussion of Fraunhofer diffraction can be found elsewhere. Template:TOC limit

Definition

When a beam of light is partly blocked by an obstacle, some of the light is scattered around the object, and light and dark bands are often seen at the edge of the shadow – this effect is known as diffraction. The Kirchhoff diffraction equation provides an expression, derived from the wave equation, which describes the wave diffracted by an aperture; analytical solutions to this equation are not available for most configurations.

The Fraunhofer diffraction equation is an approximation which can be applied when the diffracted wave is observed in the far field, and also when a lens is used to focus the diffracted light; in many instances, a simple analytical solution is available to the Fraunhofer equation – several of these are derived below.

In Cartesian coordinates

Diffraction geometry, showing aperture (or diffracting object) plane and image plane, with coordinate system.

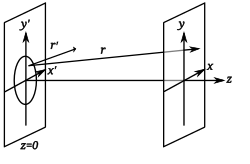
If the aperture is in Template:Math plane, with the origin in the aperture and is illuminated by a monochromatic wave, of wavelength λ, wavenumber Template:Math with complex amplitude Template:Math, and the diffracted wave is observed in the unprimed Template:Math-plane along the positive Template:Math-axis, where Template:Math are the direction cosines of the point Template:Math with respect to the origin. The complex amplitude Template:Math of the diffracted wave is given by the Fraunhofer diffraction equation as:

$$\begin{array}{cc}U(x,y,z)& \propto \underset{\text{Aperture}}{\iint }A(x^{\prime },y^{\prime })e^{-i\frac{2\pi }{\lambda }(l{x}^{\prime }+m{y}^{\prime })}d{x}^{\prime }d{y}^{\prime }\\ & \propto \underset{\text{Aperture}}{\iint }A(x^{\prime },y^{\prime })e^{-ik(l{x}^{\prime }+m{y}^{\prime })}d{x}^{\prime }d{y}^{\prime }\end{array}$$

It can be seen from this equation that the form of the diffraction pattern depends only on the direction of viewing, so the diffraction pattern changes in size but not in form with change of viewing distance.

Explicitly, the Fraunhofer diffraction equation is $$\begin{array}{c}U(x,y,z)\approx \frac{e^{ikz}{e}^{ik(x^2+y^2)/2z}}{i\lambda z}\underset{\text{Aperture}}{\iint }A(x^{\prime },y^{\prime })e^{-i\frac{k}{z}(x^{\prime }x+y^{\prime }y)}d{x}^{\prime }d{y}^{\prime }\end{array}$$ where $k=2\pi /\lambda$.

It can be seen that the integral in the above equations is the Fourier transform of the aperture function evaluated at frequencies. $$\begin{array}{cc}{f}_x& =x/(\lambda z)=l/\lambda \\ f_y& =y/(\lambda z)=m/\lambda \end{array}$$

Thus, we can also write the equation in terms of a Fourier transform as: $$U(x,y,z)\propto \hat{f}[A(x^{\prime },y^{\prime }){]}_{f_x{f}_y}$$ where Template:Math is the Fourier transform of Template:Math. The Fourier transform formulation can be very useful in solving diffraction problems.

Another form is:

$$U(𝐫)\propto \underset{\text{Aperture}}{\int }A({𝐫}^{\prime })e^{-i𝐤\cdot ({𝐫}^{\prime }-𝐫)}d{r}^{\prime }=\underset{\text{Aperture}}{\int }{a}_0({𝐫}^{\prime })e^{i\mathbf{(}{𝐤}_{\mathrm{𝟎}}\mathbf{-}𝐤\mathbf{)}\cdot ({𝐫}^{\prime }-𝐫)}d{r}^{\prime }$$

where Template:Math represent the observation point and a point in the aperture respectively, Template:Math and Template:Math represent the wave vectors of the disturbance at the aperture and of the diffracted waves respectively, and Template:Math represents the magnitude of the disturbance at the aperture.

In polar coordinates

When the diffracting aperture has circular symmetry, it is useful to use polar rather than Cartesian coordinates.

A point in the aperture has coordinates Template:Math giving: $$x^{\prime }={\rho }^{\prime }\cos {\omega }^{\prime };y^{\prime }={\rho }^{\prime }\sin {\omega }^{\prime }$$ and $$x=\rho \cos \omega ;y=\rho \sin \omega$$

The complex amplitude at Template:Math is given by Template:Math, and the area Template:Math converts to ρ′ dρ′ dω′, giving $$\begin{array}{cc}U(\rho ,\omega ,z)& \propto \underset{0}{\overset{\mathrm{\infty }}{\int }}\underset{0}{\overset{2\pi }{\int }}A({\rho }^{\prime })e^{-i\frac{2\pi }{\lambda z}(\rho {\rho }^{\prime }\cos \omega \cos {\omega }^{\prime }+\rho {\rho }^{\prime }\sin \omega \sin {\omega }^{\prime })}{\rho }^{\prime }d{\rho }^{\prime }d{\omega }^{\prime }\\ & \propto \underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{\mathrm{\infty }}{\int }}A({\rho }^{\prime })e^{-i\frac{2\pi }{\lambda z}\rho {\rho }^{\prime }\cos (\omega -{\omega }^{\prime })}d{\omega }^{\prime }{\rho }^{\prime }d{\rho }^{\prime }\end{array}$$

Using the integral representation of the Bessel function: $$J_0(p)=\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}{e}^{ip\cos \alpha }d\alpha$$ we have $$U(\rho ,z)\propto 2\pi \underset{0}{\overset{\mathrm{\infty }}{\int }}A({\rho }^{\prime })J_0\left(\frac{2\pi {\rho }^{\prime }\rho }{\lambda z}\right){\rho }^{\prime }d{\rho }^{\prime }$$

where the integration over Template:Mvar gives Template:Math since the equation is circularly symmetric, i.e. there is no dependence on Template:Mvar.

In this case, we have Template:Math equal to the Fourier–Bessel or Hankel transform of the aperture function, Template:Math

Example

Here are given examples of Fraunhofer diffraction with a normally incident monochromatic plane wave.

In each case, the diffracting object is located in the Template:Math plane, and the complex amplitude of the incident plane wave is given by $$A(x^{\prime },y^{\prime })=a{e}^{i2\pi ct/\lambda }=a{e}^{ikct}$$ where

• Template:Mvar is the magnitude of the wave disturbance,
• Template:Mvar is the wavelength,
• Template:Math is the velocity of light,
• Template:Mvar is the time
• Template:Math = Template:Math is the wave number

and the phase is zero at time Template:Math.

The time dependent factor is omitted throughout the calculations, as it remains constant, and is averaged out when the intensity is calculated. The intensity at Template:Math is proportional to the amplitude times its complex conjugate $$I(𝐫)\propto U(𝐫)\bar{U}(𝐫)$$

These derivations can be found in most standard optics books, in slightly different forms using varying notations. A reference is given for each of the systems modelled here. The Fourier transforms used can be found here.

Narrow rectangular slit

Graph and image of single-slit diffraction

The aperture is a slit of width Template:Math which is located along the Template:Math-axis,

Solution by integration

Assuming the centre of the slit is located at Template:Math, the first equation above, for all values of Template:Mvar, is: $$\begin{array}{cc}U(x,z)& =a\underset{-W/2}{\overset{W/2}{\int }}{e}^{-2\pi ix{x}^{\prime }/(\lambda z)}d{x}^{\prime }\\ & =-\frac{a\lambda z}{2\pi ix}{\left[e^{-2\pi ix{x}^{\prime }/(\lambda z)}\right]}_{-W/2}^{W/2}\end{array}$$

Using Euler's formula, this can be simplified to: $$\begin{array}{cc}U(x,z)& =aW\frac{\sin \left[\frac{\pi Wx}{\lambda z}\right]}{\frac{\pi Wx}{\lambda z}}\\ & =aW\mathrm{sinc}\frac{\pi Wx}{\lambda z}\end{array}$$

where Template:Math. The sinc function is sometimes defined as Template:Math and this may cause confusion when looking at derivations in different texts.

This can also be written as: $$U(\theta )=aW\mathrm{sinc}\left[\frac{\pi W\sin \theta }{\lambda }\right]$$ where Template:Mvar is the angle between z-axis and the line joining Template:Mvar to the origin and Template:Math when Template:Math.

Fourier transform solution

The slit can be represented by the rect function as: $$\mathrm{rect}\left(\frac{x}{W}\right)$$

The Fourier transform of this function is given by $$\hat{f}(\mathrm{rect}(ax))=\frac{1}{|a|}\cdot \mathrm{sinc}\left(\frac{\xi }{a}\right)$$ where Template:Mvar is the Fourier transform frequency, and the Template:Math function is here defined as Template:Math

The Fourier transform frequency here is Template:Math, giving $$\begin{array}{cc}U(x,z)& \propto W\frac{\sin \frac{\pi Wx}{\lambda z}}{\frac{\pi Wx}{\lambda z}}\\ & \propto W\mathrm{sinc}\frac{\pi Wx}{\lambda z}\\ & \propto W\mathrm{sinc}\frac{\pi W\sin \theta }{\lambda }\\ & \propto W\mathrm{sinc}(kW\sin \theta /2)\end{array}$$

Note that the Template:Math function is here defined as Template:Math to maintain consistency.

Intensity

The intensity is proportional to the square of the amplitude, and is therefore $$\begin{array}{cc}I(\theta )& \propto {\mathrm{sinc}}^2\left[\frac{\pi W\sin \theta }{\lambda }\right]\\ & \propto {\mathrm{sinc}}^2\left[\frac{kW\sin \theta }{2}\right]\end{array}$$

Apertures

Rectangular aperture

Computer simulation of Fraunhofer diffraction by a rectangular aperture

When a rectangular slit of width W and height H is illuminated normally (the slit illuminated at the normal angle) by a monochromatic plane wave of wavelength Template:Mvar, the complex amplitude can be found using similar analyses to those in the previous section, applied over two independent orthogonal dimensions as:

$$\begin{array}{cc}U(x,y)& \propto \mathrm{sinc}\left(\frac{\pi Wx}{\lambda R}\right)\mathrm{sinc}\left(\frac{\pi Hy}{\lambda R}\right)\\ & \propto \mathrm{sinc}\left(\frac{kWx}{2R}\right)\mathrm{sinc}\left(\frac{kHy}{2R}\right).\end{array}$$

The intensity is given by $$\begin{array}{cc}I(x,y)& \propto {\mathrm{sinc}}^2\left(\frac{\pi Wx}{\lambda R}\right){\mathrm{sinc}}^2\left(\frac{\pi Hy}{\lambda R}\right)\\ & \propto {\mathrm{sinc}}^2\left(\frac{kWx}{2R}\right){\mathrm{sinc}}^2\left(\frac{kHy}{2R}\right)\end{array}$$

where the Template:Math and Template:Math axes define the transverse directions on the plane of observation or the image plane (described in the above figure), and Template:Math is the distance between the slit center and the point of observation $P=(x,y)$ on the image plane.

In practice, all slits are of finite size so produce diffraction on the both transverse directions, along the Template:Math (width W defined) and Template:Math (height H defined) axes. If the height H of the slit is much greater than its width W, then the spacing of the vertical (along the height or the Template:Math axis) diffraction fringes is much less than the spacing of the horizontal (along the width or Template:Math axis) fringes. If the vertical fringe spacing is so less by a relatively so large H, then the observation of the vertical fringes is so hard that a person observing the diffracted wave intensity pattern on the plane of observation or the image plane recognizes only the horizontal fringes with their narrow height. This is the reason why a height-long slit or slit array such as a diffraction grating is typically analyzed only in the dimension along the width. If the illuminating beam does not illuminate the whole height of the slit, then the spacing of the vertical fringes is determined by the dimension of the laser beam along the slit height. Close examination of the two-slit pattern below shows that there are very fine vertical diffraction fringes above and below the main spots, as well as the more obvious horizontal fringes.

Circular aperture

Airy diffraction pattern

The aperture has diameter Template:Math. The complex amplitude in the observation plane is given by

$$U(\rho ,z)=2\pi a\underset{0}{\overset{W/2}{\int }}{J}_0\left(\frac{2\pi {\rho }^{\prime }\rho }{\lambda z}\right){\rho }^{\prime }d{\rho }^{\prime }$$

Solution by integration

Using the recurrence relationship $$\frac{d}{dx}[x^{n+1}{J}_{n+1}(x)]=x^{n+1}{J}_n(x)$$ to give $$\underset{0}{\overset{x}{\int }}{x}^{\prime }{J}_0(x^{\prime })d{x}^{\prime }=x{J}_1(x)$$

If we substitute $$x^{\prime }=\frac{2\pi \rho }{\lambda z}{\rho }^{\prime }$$ and the limits of the integration become 0 and Template:Math, we get $$U(\rho ,z)\propto \frac{J_1(\pi W\rho /\lambda z)}{\pi W\rho /\lambda z}$$

Putting Template:Math, we get $$U(\theta )\propto \frac{J_1(\pi W\sin \theta /\lambda )}{\pi W\sin \theta /\lambda }$$

Solution using Fourier–Bessel transform

We can write the aperture function as a step function $$\mathrm{\Pi }(W/2)$$

The Fourier–Bessel transform for this function is given by the relationship $$F[\mathrm{\Pi }(r/a)]=\frac{2\pi J_1(qa)}{q}$$ where Template:Math is the transform frequency which is equal to Template:Math and Template:Math.

Thus, we get $$\begin{array}{cc}U(\rho )& =\frac{2\pi J_1(\pi W\rho /\lambda z)}{2\pi W\rho /\lambda z}\\ & =\frac{2\pi J_1(\pi W\sin \theta /\lambda )}{W\sin \theta /\lambda }\\ & =\frac{2\pi J_1(kW\sin \theta /2)}{kW\sin \theta /2}\end{array}$$

Intensity

The intensity is given by: $$\begin{array}{cc}I(\theta )& \propto {\left[\frac{J_1(\pi W\sin \theta /\lambda )}{(\pi W\sin \theta /\lambda )}\right]}^2\\ & \propto {\left[\frac{J_1(kW\sin \theta /2)}{(kW\sin \theta /2)}\right]}^2\end{array}$$

Form of the diffraction pattern

This known as the Airy diffraction pattern

The diffracted pattern is symmetric about the normal axis.

Aperture with a Gaussian profile

Intensity of a plane wave diffracted through an aperture with a Gaussian profile

An aperture with a Gaussian profile, for example, a photographic slide whose transmission has a Gaussian variation, so that the amplitude at a point in the aperture located at a distance r' from the origin is given by

$$A({\rho }^{\prime })=\exp (-{\left[\frac{{\rho }^{\prime }}{\sigma }\right]}^2)$$ giving $$U(\rho ,z)=2\pi a\underset{0}{\overset{\mathrm{\infty }}{\int }}\exp (-{\left[\frac{{\rho }^{\prime }}{\sigma }\right]}^2)J_0\left(\frac{2\pi {\rho }^{\prime }\rho }{\lambda z}\right){\rho }^{\prime }d{\rho }^{\prime }$$

Solution using Fourier–Bessel transform

The Fourier–Bessel or Hankel transform is defined as $$F_{\nu }(k)=\underset{0}{\overset{\mathrm{\infty }}{\int }}f(r)J_{\nu }(kr)rdr$$ where Template:Math is the Bessel function of the first kind of order Template:Mvar with Template:Math.

The Hankel transform is $$F_{\nu }\left[e^{(ar{)}^2/2}\right]=\frac{e^{-k^2/2a^2}}{a^2}$$ giving $$U(\rho ,z)\propto e^{-{\left[\frac{\pi \rho \sigma }{\lambda z}\right]}^2}$$ and $$U(\theta )\propto e^{-{\left[\frac{\pi \sigma \sin \theta }{\lambda }\right]}^2}$$

Intensity

The intensity is given by: $$I(\theta )\propto e^{-\frac{2\pi \sigma \sin \theta }{\lambda }}$$

This function is plotted on the right, and it can be seen that, unlike the diffraction patterns produced by rectangular or circular apertures, it has no secondary rings. This can be used in a process called apodization - the aperture is covered by a filter whose transmission varies as a Gaussian function, giving a diffraction pattern with no secondary rings.

Slits

Two slits

The pattern which occurs when light diffracted from two slits overlaps is of considerable interest in physics, firstly for its importance in establishing the wave theory of light through Young's interference experiment, and secondly because of its role as a thought experiment in double-slit experiment in quantum mechanics.

Narrow slits

Geometry of two slit diffraction

Two slit interference using a red laser

Assume we have two long slits illuminated by a plane wave of wavelength Template:Mvar. The slits are in the Template:Math plane, parallel to the Template:Math axis, separated by a distance Template:Math and are symmetrical about the origin. The width of the slits is small compared with the wavelength.

Solution by integration

The incident light is diffracted by the slits into uniform spherical waves. The waves travelling in a given direction Template:Mvar from the two slits have differing phases. The phase of the waves from the upper and lower slits relative to the origin is given by Template:Math and Template:Math

The complex amplitude of the summed waves is given by: $$\begin{array}{cc}U(\theta )& =a{e}^{\frac{i\pi S\sin \theta }{\lambda }}+a{e}^{-\frac{i\pi S\sin \theta }{\lambda }}\\ & =a(\cos \frac{\pi S\sin \theta }{\lambda }+i\sin \frac{\pi S\sin \theta }{\lambda })+a(\cos \frac{\pi S\sin \theta }{\lambda }-i\sin \frac{\pi S\sin \theta }{\lambda })\\ & =2a\cos \frac{\pi S\sin \theta }{\lambda }\end{array}$$

Solution using Fourier transform

The aperture can be represented by the function: $$a[\delta (x-S/2)+\delta (x+S/2)]$$ where Template:Math is the delta function.

We have $$\hat{f}[\delta (x)]=1$$ and $$\hat{f}[g(x-a)]=e^{-2\pi ia{f}_x}\hat{f}[g(x)]$$ giving $$\begin{array}{cc}U(x,z)& =\hat{f}[\delta (x-S/2)+\delta (x+S/2)]\\ & =e^{-i\pi Sx/2\lambda }+e^{i\pi Sx/2\lambda }\\ & =2\cos \frac{\pi Sx}{2\lambda }\end{array}$$

$$U(\theta )=2\cos \frac{\pi S\sin \theta }{2\lambda }$$

This is the same expression as that derived above by integration.

Intensity

This gives the intensity of the combined waves as: $$\begin{array}{cc}I(\theta )& \propto {\cos }^2\left[\frac{\pi S\sin \theta }{\lambda }\right]\\ & \propto {\cos }^2\left[\frac{kS\sin \theta }{2}\right]\end{array}$$

Slits of finite width

Single and double slit diffraction – slit separation is 0.7mm and the slit width is 0.1mm

The width of the slits, Template:Math is finite.

Solution by integration

The diffracted pattern is given by: $$\begin{array}{cc}U(\theta )& =a[e^{\frac{i\pi S\sin \theta }{\lambda }}+e^{-\frac{i\pi S\sin \theta }{\lambda }}]\underset{-W/2}{\overset{W/2}{\int }}{e}^{-2\pi i{x}^{\prime }\sin \theta /\lambda }d{x}^{\prime }\\ & =2a\cos \frac{\pi S\sin \theta }{\lambda }W\mathrm{sinc}\frac{\pi W\sin \theta }{\lambda }\end{array}$$

Solution using Fourier transform

The aperture function is given by: $$a[\mathrm{rect}\left(\frac{x-S/2}{W}\right)+\mathrm{rect}\left(\frac{x+S/2}{W}\right)]$$

The Fourier transform of this function is given by $$\hat{f}(\mathrm{rect}(ax))=\frac{1}{|a|}\cdot \mathrm{sinc}\left(\frac{\xi }{2a}\right)$$ where Template:Mvar is the Fourier transform frequency, and the Template:Math function is here defined as Template:Math and $$\hat{f}[g(x-a)]=e^{-2\pi ia{f}_x}\hat{f}[g(x)]$$

We have $$\begin{array}{cc}U(x,z)& =\hat{f}\left[a[\mathrm{rect}\left(\frac{x-S/2}{W}\right)+\mathrm{rect}\left(\frac{x+S/2}{W}\right)]\right]\\ & =2W[e^{-i\pi Sx/\lambda z}+e^{i\pi Sx/\lambda z}]\frac{\sin \frac{\pi Wx}{\lambda z}}{\frac{\pi Wx}{\lambda z}}\\ & =2a\cos \frac{\pi Sx}{\lambda z}W\mathrm{sinc}\frac{\pi Wx}{\lambda z}\end{array}$$ or $$U(\theta )=2a\cos \frac{\pi S\sin \theta }{\lambda }W\mathrm{sinc}\frac{\pi W\sin \theta }{\lambda }$$

This is the same expression as was derived by integration.

Intensity

The intensity is given by: $$\begin{array}{cc}I(\theta )& \propto {\cos }^2\left[\frac{\pi S\sin \theta }{\lambda }\right]{\mathrm{sinc}}^2\left[\frac{\pi W\sin \theta }{\lambda }\right]\\ & \propto {\cos }^2\left[\frac{kS\sin \theta }{2}\right]{\mathrm{sinc}}^2\left[\frac{kW\sin \theta }{2}\right]\end{array}$$

It can be seen that the form of the intensity pattern is the product of the individual slit diffraction pattern, and the interference pattern which would be obtained with slits of negligible width. This is illustrated in the image at the right which shows single slit diffraction by a laser beam, and also the diffraction/interference pattern given by two identical slits.

Gratings

A grating is defined in Principles of Optics by Born and Wolf as "any arrangement which imposes on an incident wave a periodic variation of amplitude or phase, or both".

Narrow slit grating

A simple grating consists of a screen with Template:Mvar slits whose width is significantly less than the wavelength of the incident light with slit separation of Template:Math.

Solution by integration

The complex amplitude of the diffracted wave at an angle Template:Mvar is given by: $$\begin{array}{cc}U(\theta )& =a\sum _{n=1}^N{e}^{\frac{-i2\pi nS\sin \theta }{\lambda }}\\ & =\frac{1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}\end{array}$$

since this is the sum of a geometric series.

Solution using Fourier transform

The aperture is given by $$\sum _{n=0}^N\delta (x-nS)$$

The Fourier transform of this function is: $$\begin{array}{cc}\hat{f}[\sum _{n=0}^N\delta (x-nS)]& =\sum _{n=0}^N{e}^{-i{f}_{x}nS}\\ & =\frac{1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}\end{array}$$

Intensity

Diffraction pattern for 50 narrow-slit grating

Detail of main maximum in 20 and 50 narrow slit grating diffraction patterns

The intensity is given by:

$$\begin{array}{cc}I(\theta )& \propto \frac{1-\cos (2\pi NS\sin \theta /\lambda )}{1-\cos (2\pi S\sin \theta /\lambda )}\\ & \propto \frac{{\sin }^2(\pi NS\sin \theta /\lambda )}{{\sin }^2(\pi S\sin \theta /\lambda )}\end{array}$$

This function has a series of maxima and minima. There are regularly spaced "principal maxima", and a number of much smaller maxima in between the principal maxima. The principal maxima occur when $$\pi S{\sin }_n\theta /\lambda =n\pi ,n=0,\pm 1,\pm 2,\dots$$ and the main diffracted beams therefore occur at angles: $$\sin {\theta }_n=\frac{n\lambda }{S},n=0,\pm 1\pm 2,\dots$$

This is the grating equation for normally incident light.

The number of small intermediate maxima is equal to the number of slits, Template:Math and their size and shape is also determined by Template:Math.

The form of the pattern for Template:Math=50 is shown in the first figure .

The detailed structure for 20 and 50 slits gratings are illustrated in the second diagram.

Finite width slit grating

Diffraction pattern from grating with finite width slits

The grating now has N slits of width Template:Math and spacing Template:Math

Solution using integration

The amplitude is given by: $$\begin{array}{cc}U(\theta ,\varphi )& \propto a\sum _{n=1}^N{e}^{\frac{-i2\pi nS\sin \theta }{\lambda }}\underset{-W/2}{\overset{W/2}{\int }}{e}^{-2\pi ix{x}^{\prime }/(\lambda z)}d{x}^{\prime }\\ & \propto a\mathrm{sinc}\left(\frac{\pi W\sin \theta }{\lambda }\right)\frac{1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}\end{array}$$

Solution using Fourier transform

The aperture function can be written as: $$\sum _{n=1}^N\mathrm{rect}\left[\frac{x^{\prime }-nS}{W}\right]$$

Using the convolution theorem, which says that if we have two functions Template:Math and Template:Math, and we have $$h(x)=(f*g)(x)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(y)g(x-y)dy,$$ where Template:Math denotes the convolution operation, then we also have $$\hat{h}(\xi )=\hat{f}(\xi )\cdot \hat{g}(\xi ).$$ we can write the aperture function as $$\mathrm{rect}(x^{\prime }/W)*\sum _{n=0}^N\delta (x^{\prime }-nS)$$

The amplitude is then given by the Fourier transform of this expression as: $$\begin{array}{cc}U(x,z)& =\hat{f}[\mathrm{rect}(x^{\prime }/W)]\hat{f}[\sum _{n=0}^N\delta (x^{\prime }-nS)]\\ & =a\mathrm{sinc}\left(\frac{W\sin \theta }{\lambda }\right)\frac{1-e^{-i2\pi NS\sin \theta /\lambda }}{1-e^{-i2\pi S\sin \theta /\lambda }}\end{array}$$

Intensity

The intensity is given by: $$I(\theta )\propto {\mathrm{sinc}}^2\left(\frac{\pi W\sin \theta }{\lambda }\right)\frac{{\sin }^2(\pi NS\sin \theta /\lambda )}{{\sin }^2(\pi S\sin \theta /\lambda )}$$

The diagram shows the diffraction pattern for a grating with 20 slits, where the width of the slits is 1/5th of the slit separation. The size of the main diffracted peaks is modulated with the diffraction pattern of the individual slits.

Other gratings

The Fourier transform method above can be used to find the form of the diffraction for any periodic structure where the Fourier transform of the structure is known. Goodman uses this method to derive expressions for the diffraction pattern obtained with sinusoidal amplitude and phase modulation gratings. These are of particular interest in holography.

Extensions

Non-normal illumination

If the aperture is illuminated by a monochromatic plane wave incident in a direction Template:Math, the first version of the Fraunhofer equation above becomes: $$\begin{array}{cc}U(x,y,z)& \propto \underset{\text{Aperture}}{\iint }A(x^{\prime },y^{\prime })e^{-i\frac{2\pi }{\lambda }[(l-l_0)x^{\prime }+(m-m_0)y^{\prime }]}d{x}^{\prime }d{y}^{\prime }\\ & \propto \underset{\text{Aperture}}{\iint }A(x^{\prime },y^{\prime })e^{-ik[(l-l_0)x^{\prime }+(m-m_0)y^{\prime }]}d{x}^{\prime }d{y}^{\prime }\end{array}$$

The equations used to model each of the systems above are altered only by changes in the constants multiplying Template:Math and Template:Math, so the diffracted light patterns will have the form, except that they will now be centred around the direction of the incident plane wave.

The grating equation becomes $$\sin {\theta }_n=\frac{n\lambda }{S}+\sin {\theta }_0,n=0,\pm 1,\pm 2,\dots$$

Non-monochromatic illumination

In all of the above examples of Fraunhofer diffraction, the effect of increasing the wavelength of the illuminating light is to reduce the size of the diffraction structure, and conversely, when the wavelength is reduced, the size of the pattern increases. If the light is not mono-chromatic, i.e. it consists of a range of different wavelengths, each wavelength is diffracted into a pattern of a slightly different size to its neighbours. If the spread of wavelengths is significantly smaller than the mean wavelength, the individual patterns will vary very little in size, and so the basic diffraction will still appear with slightly reduced contrast. As the spread of wavelengths is increased, the number of "fringes" which can be observed is reduced.

See also

• Kirchhoff's diffraction formula
• Fresnel diffraction
• Huygens principle
• Airy disc
• Fourier optics

References

• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite journal