Orchard-planting problem

An arrangement of nine points (related to the Pappus configuration) forming ten 3-point lines.

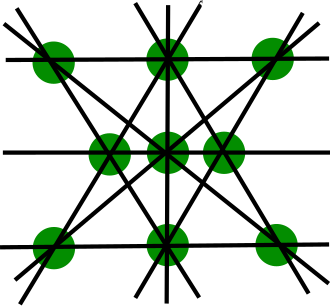
In discrete geometry, the original orchard-planting problem (or the tree-planting problem) asks for the maximum number of 3-point lines attainable by a configuration of a specific number of points in the plane. There are also investigations into how many Template:Mvar-point lines there can be. Hallard T. Croft and Paul Erdős proved $$t_k>\frac{c{n}^2}{k^3},$$ where Template:Mvar is the number of points and Template:Mvar is the number of Template:Mvar-point lines. Their construction contains some Template:Mvar-point lines, where Template:Math. One can also ask the question if these are not allowed.

Integer sequence

Define Template:Tmath to be the maximum number of 3-point lines attainable with a configuration of Template:Mvar points. For an arbitrary number of Template:Mvar points, Template:Tmath was shown to be $\frac{1}{6}{n}^2-O(n)$ in 1974.

The first few values of Template:Tmath are given in the following table Template:OEIS.

Template:Mvar	4	5	6	7	8	9	10	11	12	13	14
Template:Tmath	1	2	4	6	7	10	12	16	19	22	26

Upper and lower bounds

Since no two lines may share two distinct points, a trivial upper-bound for the number of 3-point lines determined by Template:Mvar points is $$\lfloor (\genfrac{}{}{0ex}{}{n}{2})/(\genfrac{}{}{0ex}{}{3}{2})\rfloor =\lfloor \frac{n^2-n}{6}\rfloor .$$ Using the fact that the number of 2-point lines is at least Template:Tmath Template:Harv, this upper bound can be lowered to $$\lfloor \frac{(\genfrac{}{}{0ex}{}{n}{2})-\frac{6n}{13}}{3}\rfloor =\lfloor \frac{n^2}{6}-\frac{25n}{78}\rfloor .$$

Lower bounds for Template:Tmath are given by constructions for sets of points with many 3-point lines. The earliest quadratic lower bound of $\approx \frac{1}{8}{n}^2$ was given by Sylvester, who placed Template:Mvar points on the cubic curve Template:Math. This was improved to $\frac{1}{6}{n}^2-\frac{1}{2}n+1$ in 1974 by Template:Harvs, using a construction based on Weierstrass's elliptic functions. An elementary construction using hypocycloids was found by Template:Harvtxt achieving the same lower bound.

In September 2013, Ben Green and Terence Tao published a paper in which they prove that for all point sets of sufficient size, Template:Math, there are at most $$\frac{n(n-3)}{6}+1=\frac{1}{6}{n}^2-\frac{1}{2}n+1$$ 3-point lines which matches the lower bound established by Burr, Grünbaum and Sloane. Thus, for sufficiently large Template:Mvar, the exact value of Template:Tmath is known.

This is slightly better than the bound that would directly follow from their tight lower bound of Template:Tmath for the number of 2-point lines: $\frac{n(n-2)}{6},$ proved in the same paper and solving a 1951 problem posed independently by Gabriel Andrew Dirac and Theodore Motzkin.

Orchard-planting problem has also been considered over finite fields. In this version of the problem, the Template:Mvar points lie in a projective plane defined over a finite field. Template:Harv.

References

• Template:Citation.
• Template:Citation.
• Template:Citation.
• Template:Citation.
• Template:Citation
• Template:Citation

External links

• Template:MathWorld