Kontsevich quantization formula

In mathematics, the Kontsevich quantization formula describes how to construct a generalized ★-product operator algebra from a given arbitrary finite-dimensional Poisson manifold. This operator algebra amounts to the deformation quantization of the corresponding Poisson algebra. It is due to Maxim Kontsevich.

Deformation quantization of a Poisson algebra

Given a Poisson algebra Template:Math, a deformation quantization is an associative unital product $\star$ on the algebra of formal power series in Template:Math, subject to the following two axioms,

$\begin{array}{cc}f\star g& =fg+𝒪(\hslash )\\ [f,g]& =f\star g-g\star f=i\hslash \{f,g\}+𝒪({\hslash }^2)\end{array}$

If one were given a Poisson manifold Template:Math, one could ask, in addition, that

$f\star g=fg+\sum _{k=1}^{\mathrm{\infty }}{\hslash }^k{B}_k(f\otimes g),$

where the Template:Mvar are linear bidifferential operators of degree at most Template:Mvar.

Two deformations are said to be equivalent iff they are related by a gauge transformation of the type,

$\{\begin{array}{c}D:A[[\hslash ]]\to A[[\hslash ]]\\ \sum _{k=0}^{\mathrm{\infty }}{\hslash }^k{f}_k\mapsto \sum _{k=0}^{\mathrm{\infty }}{\hslash }^k{f}_k+\sum _{n\ge 1,k\ge 0}{D}_n(f_k){\hslash }^{n+k}\end{array}$

where Template:Mvar are differential operators of order at most Template:Mvar. The corresponding induced $\star$-product, ${\star }^{\prime }$, is then

$f{\star }^{\prime }g=D(\left(D^{-1}f\right)\star \left(D^{-1}g\right)).$

For the archetypal example, one may well consider Groenewold's original "Moyal–Weyl" $\star$-product.

Kontsevich graphs

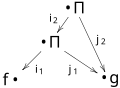
A Kontsevich graph is a simple directed graph without loops on 2 external vertices, labeled f and g; and Template:Mvar internal vertices, labeled Template:Math. From each internal vertex originate two edges. All (equivalence classes of) graphs with Template:Mvar internal vertices are accumulated in the set Template:Math.

An example on two internal vertices is the following graph,

Associated bidifferential operator

Associated to each graph Template:Math, there is a bidifferential operator Template:Math defined as follows. For each edge there is a partial derivative on the symbol of the target vertex. It is contracted with the corresponding index from the source symbol. The term for the graph Template:Math is the product of all its symbols together with their partial derivatives. Here f and g stand for smooth functions on the manifold, and Template:Math is the Poisson bivector of the Poisson manifold.

The term for the example graph is

${\mathrm{\Pi }}^{i_2{j}_2}{\partial }_{i_2}{\mathrm{\Pi }}^{i_1{j}_1}{\partial }_{i_1}f{\partial }_{j_1}{\partial }_{j_2}g.$

Associated weight

For adding up these bidifferential operators there are the weights Template:Math of the graph Template:Math. First of all, to each graph there is a multiplicity Template:Math which counts how many equivalent configurations there are for one graph. The rule is that the sum of the multiplicities for all graphs with Template:Mvar internal vertices is Template:Math. The sample graph above has the multiplicity Template:Math. For this, it is helpful to enumerate the internal vertices from 1 to Template:Mvar.

In order to compute the weight we have to integrate products of the angle in the upper half-plane, H, as follows. The upper half-plane is Template:Math, endowed with the Poincaré metric

$d{s}^2=\frac{d{x}^2+d{y}^2}{y^2};$

and, for two points Template:Math with Template:Math, we measure the angle Template:Mvar between the geodesic from Template:Mvar to Template:Math and from Template:Mvar to Template:Mvar counterclockwise. This is

$\varphi (z,w)=\frac{1}{2i}\log \frac{(z-w)(z-\overline{w})}{(\overline{z}-w)(\overline{z}-\overline{w})}.$

The integration domain is C_n(H) the space

$C_n(H):=\{(u_1,\dots ,u_n)\in H^n:u_i\ne u_j\mathrm{\forall }i\ne j\}.$

The formula amounts

$w_{\mathrm{\Gamma }}:=\frac{m(\mathrm{\Gamma })}{(2\pi {)}^{2n}n!}\underset{C_n(H)}{\int }\underset{j=1}{\overset{n}{\bigwedge }}\mathrm{d}\varphi (u_j,u_{t1(j)})\wedge \mathrm{d}\varphi (u_j,u_{t2(j)})$,

where t1(j) and t2(j) are the first and second target vertex of the internal vertex Template:Mvar. The vertices f and g are at the fixed positions 0 and 1 in Template:Mvar.

The formula

Given the above three definitions, the Kontsevich formula for a star product is now

$f\star g=fg+\sum _{n=1}^{\mathrm{\infty }}{\left(\frac{i\hslash }{2}\right)}^n\sum _{\mathrm{\Gamma }\in G_n(2)}{w}_{\mathrm{\Gamma }}{B}_{\mathrm{\Gamma }}(f\otimes g).$

Explicit formula up to second order

Enforcing associativity of the $\star$-product, it is straightforward to check directly that the Kontsevich formula must reduce, to second order in Template:Mvar, to just

$\begin{array}{cc}f\star g& =fg+\frac{i\hslash }{2}{\mathrm{\Pi }}^{ij}{\partial }_{i}f{\partial }_{j}g-\frac{{\hslash }^2}{8}{\mathrm{\Pi }}^{i_1{j}_1}{\mathrm{\Pi }}^{i_2{j}_2}{\partial }_{i_1}{\partial }_{i_2}f{\partial }_{j_1}{\partial }_{j_2}g\\ & -\frac{{\hslash }^2}{12}{\mathrm{\Pi }}^{i_1{j}_1}{\partial }_{j_1}{\mathrm{\Pi }}^{i_2{j}_2}({\partial }_{i_1}{\partial }_{i_2}f{\partial }_{j_2}g-{\partial }_{i_2}f{\partial }_{i_1}{\partial }_{j_2}g)+𝒪({\hslash }^3)\end{array}$