Blossom algorithm

In graph theory, the blossom algorithm is an algorithm for constructing maximum matchings on graphs. The algorithm was developed by Jack Edmonds in 1961, and published in 1965. Given a general graph Template:Math, the algorithm finds a matching Template:Mvar such that each vertex in Template:Mvar is incident with at most one edge in Template:Mvar and Template:Math is maximized. The matching is constructed by iteratively improving an initial empty matching along augmenting paths in the graph. Unlike bipartite matching, the key new idea is that an odd-length cycle in the graph (blossom) is contracted to a single vertex, with the search continuing iteratively in the contracted graph.

The algorithm runs in time Template:Math, where Template:Math is the number of edges of the graph and Template:Math is its number of vertices. A better running time of $O(|E|\sqrt{|V|})$ for the same task can be achieved with the much more complex algorithm of Micali and Vazirani.

A major reason that the blossom algorithm is important is that it gave the first proof that a maximum-size matching could be found using a polynomial amount of computation time. Another reason is that it led to a linear programming polyhedral description of the matching polytope, yielding an algorithm for min-weight matching. As elaborated by Alexander Schrijver, further significance of the result comes from the fact that this was the first polytope whose proof of integrality "does not simply follow just from total unimodularity, and its description was a breakthrough in polyhedral combinatorics."

Augmenting paths

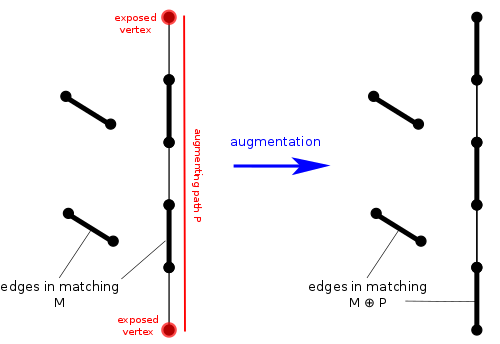
Given Template:Math and a matching Template:Mvar of Template:Mvar, a vertex Template:Mvar is exposed if no edge of Template:Mvar is incident with Template:Mvar. A path in Template:Mvar is an alternating path, if its edges are alternately not in Template:Mvar and in Template:Mvar (or in Template:Mvar and not in Template:Mvar). An augmenting path Template:Mvar is an alternating path that starts and ends at two distinct exposed vertices. Note that the number of unmatched edges in an augmenting path is greater by one than the number of matched edges, and hence the total number of edges in an augmenting path is odd. A matching augmentation along an augmenting path Template:Mvar is the operation of replacing Template:Mvar with a new matching

$M_1=M\oplus P=(M\setminus P)\cup (P\setminus M)$.

By Berge's lemma, matching Template:Mvar is maximum if and only if there is no Template:Mvar-augmenting path in Template:Mvar. Hence, either a matching is maximum, or it can be augmented. Thus, starting from an initial matching, we can compute a maximum matching by augmenting the current matching with augmenting paths as long as we can find them, and return whenever no augmenting paths are left. We can formalize the algorithm as follows:

   INPUT:  Graph G, initial matching M on G
   OUTPUT: maximum matching M* on G
A1 function find_maximum_matching(G, M) : M*
A2     P ← find_augmenting_path(G, M)
A3     if P is non-empty then
A4         return find_maximum_matching(G, augment M along P)
A5     else
A6         return M
A7     end if
A8 end function

We still have to describe how augmenting paths can be found efficiently. The subroutine to find them uses blossoms and contractions.

Blossoms and contractions

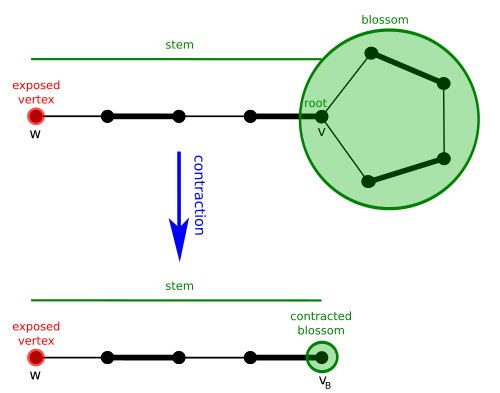
Given Template:Math and a matching Template:Mvar of Template:Mvar, a blossom Template:Mvar is a cycle in Template:Mvar consisting of Template:Math edges of which exactly Template:Mvar belong to Template:Mvar, and where one of the vertices Template:Mvar of the cycle (the base) is such that there exists an alternating path of even length (the stem) from Template:Mvar to an exposed vertex Template:Mvar.

Finding Blossoms:

• Traverse the graph starting from an exposed vertex.
• Starting from that vertex, label it as an outer vertex Template:Mvar.
• Alternate the labeling between vertices being inner Template:Mvar and outer Template:Mvar such that no two adjacent vertices have the same label.
• If we end up with two adjacent vertices labeled as outer Template:Mvar then we have an odd-length cycle and hence a blossom.

Define the contracted graph Template:Mvar as the graph obtained from Template:Mvar by contracting every edge of Template:Mvar, and define the contracted matching Template:Mvar as the matching of Template:Mvar corresponding to Template:Mvar.

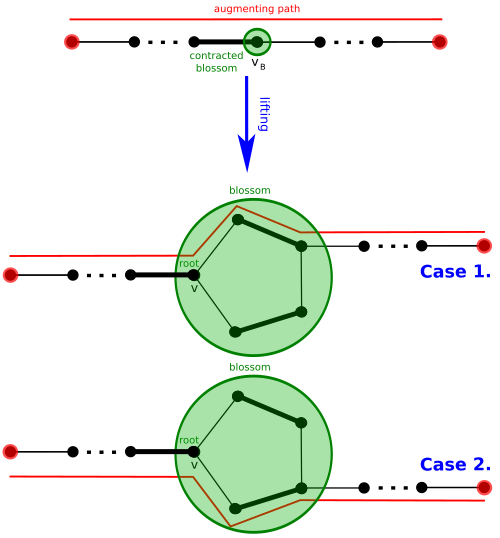
Template:Mvar has an Template:Mvar-augmenting path if and only if Template:Mvar has an Template:Mvar-augmenting path, and that any Template:Mvar-augmenting path Template:Mvar in Template:Mvar can be lifted to an Template:Mvar-augmenting path in Template:Mvar by undoing the contraction by Template:Mvar so that the segment of Template:Mvar (if any) traversing through Template:Mvar is replaced by an appropriate segment traversing through Template:Mvar. In more detail:

• if Template:Mvar traverses through a segment Template:Math in Template:Mvar, then this segment is replaced with the segment Template:Math in Template:Mvar, where blossom vertices Template:Mvar and Template:Mvar and the side of Template:Mvar, Template:Math, going from Template:Mvar to Template:Mvar are chosen to ensure that the new path is still alternating (Template:Mvar is exposed with respect to $M\cap B$, $\{w^{\prime },w\}\in E\setminus M$).

• if Template:Mvar has an endpoint Template:Mvar, then the path segment Template:Math in Template:Mvar is replaced with the segment Template:Math in Template:Mvar, where blossom vertices Template:Mvar and Template:Mvar and the side of Template:Mvar, Template:Math, going from Template:Mvar to Template:Mvar are chosen to ensure that the path is alternating (Template:Mvar is exposed, $\{u^{\prime },u\}\in E\setminus M$).

Thus blossoms can be contracted and search performed in the contracted graphs. This reduction is at the heart of Edmonds' algorithm.

Finding an augmenting path

The search for an augmenting path uses an auxiliary data structure consisting of a forest Template:Mvar whose individual trees correspond to specific portions of the graph Template:Mvar. In fact, the forest Template:Mvar is the same that would be used to find maximum matchings in bipartite graphs (without need for shrinking blossoms). In each iteration the algorithm either (1) finds an augmenting path, (2) finds a blossom and recurses onto the corresponding contracted graph, or (3) concludes there are no augmenting paths. The auxiliary structure is built by an incremental procedure discussed next.

The construction procedure considers vertices Template:Mvar and edges Template:Mvar in Template:Mvar and incrementally updates Template:Mvar as appropriate. If Template:Mvar is in a tree Template:Mvar of the forest, we let Template:Code denote the root of Template:Mvar. If both Template:Mvar and Template:Mvar are in the same tree Template:Mvar in Template:Mvar, we let Template:Code denote the length of the unique path from Template:Mvar to Template:Mvar in Template:Mvar.

    INPUT:  Graph G, matching M on G
    OUTPUT: augmenting path P in G or empty path if none found
B01 function find_augmenting_path(G, M) : P
B02    F ← empty forest
B03    unmark all vertices and edges in G, mark all edges of M
B05    for each exposed vertex v do
B06        create a singleton tree { v } and add the tree to F
B07    end for
B08    while there is an unmarked vertex v in F with distance(v, root(v)) even do
B09        while there exists an unmarked edge e = { v, w } do
B10            if w is not in F then
                   // w is matched, so add e and w's matched edge to F
B11                x ← vertex matched to w in M
B12                add edges { v, w } and { w, x } to the tree of v
B13            else
B14                if distance(w, root(w)) is odd then
                       // Do nothing.
B15                else
B16                    if root(v) ≠ root(w) then
                           // Report an augmenting path in F $\cup$ { e }.
B17                        P ← path (root(v) → ... → v) → (w → ... → root(w))
B18                        return P
B19                    else
                           // Contract a blossom in G and look for the path in the contracted graph.
B20                        B ← blossom formed by e and edges on the path v → w in T
B21                        G’, M’ ← contract G and M by B
B22                        P’ ← find_augmenting_path(G’, M’)
B23                        P ← lift P’ to G
B24                        return P
B25                    end if
B26                end if
B27            end if
B28            mark edge e
B29        end while
B30        mark vertex v
B31    end while
B32    return empty path
B33 end function

Examples

The following four figures illustrate the execution of the algorithm. Dashed lines indicate edges that are currently not present in the forest. First, the algorithm processes an out-of-forest edge that causes the expansion of the current forest (lines B10 – B12).

Next, it detects a blossom and contracts the graph (lines B20 – B21).

Finally, it locates an augmenting path Template:Mvar in the contracted graph (line B22) and lifts it to the original graph (line B23). Note that the ability of the algorithm to contract blossoms is crucial here; the algorithm cannot find Template:Mvar in the original graph directly because only out-of-forest edges between vertices at even distances from the roots are considered on line B17 of the algorithm.

Analysis

The forest Template:Mvar constructed by the Template:Code function is an alternating forest.

• a tree Template:Mvar in Template:Mvar is an alternating tree with respect to Template:Mvar, if
  • Template:Mvar contains exactly one exposed vertex Template:Mvar called the tree root
  • every vertex at an odd distance from the root has exactly two incident edges in Template:Mvar, and
  • all paths from Template:Mvar to leaves in Template:Mvar have even lengths, their odd edges are not in Template:Mvar and their even edges are in Template:Mvar.
• a forest Template:Mvar in Template:Mvar is an alternating forest with respect to Template:Mvar, if
  • its connected components are alternating trees, and
  • every exposed vertex in Template:Mvar is a root of an alternating tree in Template:Mvar.

Each iteration of the loop starting at line B09 either adds to a tree Template:Mvar in Template:Mvar (line B10) or finds an augmenting path (line B17) or finds a blossom (line B20). It is easy to see that the running time is $O(|E||V{|}^2)$.

Bipartite matching

When Template:Mvar is bipartite, there are no odd cycles in Template:Mvar. In that case, blossoms will never be found and one can simply remove lines B20 – B24 of the algorithm. The algorithm thus reduces to the standard algorithm to construct maximum cardinality matchings in bipartite graphs where we repeatedly search for an augmenting path by a simple graph traversal: this is for instance the case of the Ford–Fulkerson algorithm.

Weighted matching

The matching problem can be generalized by assigning weights to edges in Template:Mvar and asking for a set Template:Mvar that produces a matching of maximum (minimum) total weight: this is the maximum weight matching problem. This problem can be solved by a combinatorial algorithm that uses the unweighted Edmonds's algorithm as a subroutine. Kolmogorov provides an efficient C++ implementation of this.