Solution of triangles

File:Beliebiges Dreieck cen.png

A general form triangle has six main characteristics (see picture): three linear (side lengths Template:Mvar) and three angular (Template:Mvar). The classical plane trigonometry problem is to specify three of the six characteristics and determine the other three. A triangle can be uniquely determined in this sense when given any of the following:^[1]^[2]

Three sides (SSS)
Two sides and the included angle (SAS, side-angle-side)
Two sides and an angle not included between them (SSA), if the side length adjacent to the angle is shorter than the other side length.
A side and the two angles adjacent to it (ASA)
A side, the angle opposite to it and an angle adjacent to it (AAS).

For all cases in the plane, at least one of the side lengths must be specified. If only the angles are given, the side lengths cannot be determined, because any similar triangle is a solution.

Trigonomic relations

Overview of particular steps and tools used when solving plane triangles

The standard method of solving the problem is to use fundamental relations.

Law of cosines $\begin{matrix} a^{2} & = b^{2} + c^{2} - 2 b c \cos α \\ b^{2} & = a^{2} + c^{2} - 2 a c \cos β \\ c^{2} & = a^{2} + b^{2} - 2 a b \cos γ \end{matrix}$

Law of sines $\frac{a}{\sin α} = \frac{b}{\sin β} = \frac{c}{\sin γ}$
Sum of angles: $α + β + γ = 18 0^{\circ}$
Law of tangents $\frac{a - b}{a + b} = \frac{\tan \frac{1}{2} (α - β)}{\tan \frac{1}{2} (α + β)} .$

There are other (sometimes practically useful) universal relations: the law of cotangents and Mollweide's formula.

Notes

To find an unknown angle, the law of cosines is safer than the law of sines. The reason is that the value of sine for the angle of the triangle does not uniquely determine this angle. For example, if Template:Math, the angle Template:Mvar can equal either 30° or 150°. Using the law of cosines avoids this problem: within the interval from 0° to 180° the cosine value unambiguously determines its angle. On the other hand, if the angle is small (or close to 180°), then it is more robust numerically to determine it from its sine than its cosine because the arc-cosine function has a divergent derivative at 1 (or −1).
We assume that the relative position of specified characteristics is known. If not, the mirror reflection of the triangle will also be a solution. For example, three side lengths uniquely define either a triangle or its reflection.

Three sides given (SSS)

File:Resolve triangle with a b c.png

Let three side lengths Template:Mvar be specified. To find the angles Template:Mvar, the law of cosines can be used:^[3] $\begin{matrix} α & = \arccos \frac{b^{2} + c^{2} - a^{2}}{2 b c} \\ β & = \arccos \frac{a^{2} + c^{2} - b^{2}}{2 a c} . \end{matrix}$

Then angle Template:Math.

Some sources recommend to find angle Template:Mvar from the law of sines but (as Note 1 above states) there is a risk of confusing an acute angle value with an obtuse one.

Another method of calculating the angles from known sides is to apply the law of cotangents.

Area using Heron's formula: $A = \sqrt{s (s - a) (s - b) (s - c)}$ where $s = \frac{a + b + c}{2}$

Heron's formula without using the semiperimeter: $A = \frac{\sqrt{(a + b + c) (b + c - a) (a + c - b) (a + b - c)}}{4}$

Two sides and the included angle given (SAS)

File:Resolve triangle with b c beta.png

Here the lengths of sides Template:Mvar and the angle Template:Mvar between these sides are known. The third side can be determined from the law of cosines:^[4] $c = \sqrt{a^{2} + b^{2} - 2 a b \cos γ} .$ Now we use law of cosines to find the second angle: $α = \arccos \frac{b^{2} + c^{2} - a^{2}}{2 b c} .$ Finally, Template:Math.

Two sides and non-included angle given (SSA)

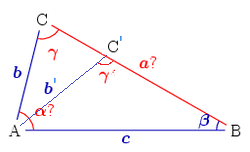
File:Solve spherical triangle with a b c.png

This case is not solvable in all cases; a solution is guaranteed to be unique only if the side length adjacent to the angle is shorter than the other side length. Assume that two sides Template:Mvar and the angle Template:Mvar are known. The equation for the angle Template:Mvar can be implied from the law of sines:^[5] $\sin γ = \frac{c}{b} \sin β .$ We denote further Template:Math (the equation's right side). There are four possible cases:

If Template:Math, no such triangle exists because the side Template:Mvar does not reach line Template:Mvar. For the same reason a solution does not exist if the angle Template:Math and Template:Math.
If Template:Math, a unique solution exists: Template:Math, i.e., the triangle is right-angled.
If Template:Math two alternatives are possible.
1. If Template:Math, then Template:Math (the larger side corresponds to a larger angle). Since no triangle can have two obtuse angles, Template:Math is an acute angle and the solution Template:Math is unique.
2. If Template:Math, the angle Template:Math may be acute: Template:Math or obtuse: Template:Math. The figure on right shows the point Template:Math, the side Template:Math and the angle Template:Math as the first solution, and the point Template:Math, side Template:Math and the angle Template:Math as the second solution.

Once Template:Math is obtained, the third angle Template:Math.

The third side can then be found from the law of sines: $a = b \frac{\sin α}{\sin β}$

or from the law of cosines: $a = c \cos β \pm \sqrt{b^{2} - c^{2} \sin^{2} β}$

A side and two adjacent angles given (ASA)

The known characteristics are the side Template:Mvar and the angles Template:Mvar. The third angle Template:Math.

Two unknown sides can be calculated from the law of sines:^[6] $\begin{matrix} a & = c \frac{\sin α}{\sin γ} = c \frac{\sin α}{\sin (α + β)} \\ b & = c \frac{\sin β}{\sin γ} = c \frac{\sin β}{\sin (α + β)} \end{matrix}$

A side, one adjacent angle and the opposite angle given (AAS)

The procedure for solving an AAS triangle is same as that for an ASA triangle: First, find the third angle by using the angle sum property of a triangle, then find the other two sides using the law of sines.

Other given lengths

In many cases, triangles can be solved given three pieces of information some of which are the lengths of the triangle's medians, altitudes, or angle bisectors. Posamentier and Lehmann^[7] list the results for the question of solvability using no higher than square roots (i.e., constructibility) for each of the 95 distinct cases; 63 of these are constructible.

Solving spherical triangles

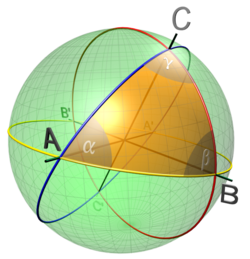
The general spherical triangle is fully determined by three of its six characteristics (3 sides and 3 angles). The lengths of the sides Template:Mvar of a spherical triangle are their central angles, measured in angular units rather than linear units. (On a unit sphere, the angle (in radians) and length around the sphere are numerically the same. On other spheres, the angle (in radians) is equal to the length around the sphere divided by the radius.)

Spherical geometry differs from planar Euclidean geometry, so the solution of spherical triangles is built on different rules. For example, the sum of the three angles Template:Math depends on the size of the triangle. In addition, similar triangles cannot be unequal, so the problem of constructing a triangle with specified three angles has a unique solution. The basic relations used to solve a problem are similar to those of the planar case: see Spherical law of cosines and Spherical law of sines.

Among other relationships that may be useful are the half-side formula and Napier's analogies:^[8] $\begin{matrix} \tan \frac{1}{2} c \cos \frac{1}{2} (α - β) & = \tan \frac{1}{2} (a + b) \cos \frac{1}{2} (α + β) \\ \tan \frac{1}{2} c \sin \frac{1}{2} (α - β) & = \tan \frac{1}{2} (a - b) \sin \frac{1}{2} (α + β) \\ \cot \frac{1}{2} γ \cos \frac{1}{2} (a - b) & = \tan \frac{1}{2} (α + β) \cos \frac{1}{2} (a + b) \\ \cot \frac{1}{2} γ \sin \frac{1}{2} (a - b) & = \tan \frac{1}{2} (α - β) \sin \frac{1}{2} (a + b) . \end{matrix}$

Three sides given (spherical SSS)

Known: the sides Template:Math (in angular units). The triangle's angles are computed using the spherical law of cosines: $\begin{matrix} α & = \arccos \frac{\cos a - \cos b \cos c}{\sin b \sin c}, \\ β & = \arccos \frac{\cos b - \cos c \cos a}{\sin c \sin a}, \\ γ & = \arccos \frac{\cos c - \cos a \cos b}{\sin a \sin b} . \end{matrix}$

Two sides and the included angle given (spherical SAS)

Known: the sides Template:Mvar and the angle Template:Mvar between them. The side Template:Mvar can be found from the spherical law of cosines: $c = \arccos (\cos a \cos b + \sin a \sin b \cos γ) .$

The angles Template:Mvar can be calculated as above, or by using Napier's analogies:

$\begin{matrix} α & = \arctan \frac{2 \sin a}{\tan \frac{1}{2} γ \sin (b + a) + \cot \frac{1}{2} γ \sin (b - a)}, \\ β & = \arctan \frac{2 \sin b}{\tan \frac{1}{2} γ \sin (a + b) + \cot \frac{1}{2} γ \sin (a - b)} . \end{matrix}$

This problem arises in the navigation problem of finding the great circle between two points on the earth specified by their latitude and longitude; in this application, it is important to use formulas which are not susceptible to round-off errors. For this purpose, the following formulas (which may be derived using vector algebra) can be used: $\begin{matrix} c & = \arctan \frac{\sqrt{(\sin a \cos b - \cos a \sin b \cos γ)^{2} + (\sin b \sin γ)^{2}}}{\cos a \cos b + \sin a \sin b \cos γ}, \\ α & = \arctan \frac{\sin a \sin γ}{\sin b \cos a - \cos b \sin a \cos γ}, \\ β & = \arctan \frac{\sin b \sin γ}{\sin a \cos b - \cos a \sin b \cos γ}, \end{matrix}$ where the signs of the numerators and denominators in these expressions should be used to determine the quadrant of the arctangent.

File:Solve spherical triangle with b c beta.png

File:Solve spherical triangle with c alpha beta.png

Two sides and non-included angle given (spherical SSA)

This problem is not solvable in all cases; a solution is guaranteed to be unique only if the side length adjacent to the angle is shorter than the other side length. Known: the sides Template:Mvar and the angle Template:Mvar not between them. A solution exists if the following condition holds: $b > \arcsin (\sin c \sin β) .$ The angle Template:Mvar can be found from the spherical law of sines: $γ = \arcsin \frac{\sin c \sin β}{\sin b} .$ As for the plane case, if Template:Math then there are two solutions: Template:Mvar and Template:Math.

We can find other characteristics by using Napier's analogies: $\begin{matrix} a & = 2 \arctan [\tan \frac{1}{2} (b - c) \frac{\sin \frac{1}{2} (β + γ)}{\sin \frac{1}{2} (β - γ)}], \\ α & = 2 arccot [\tan \frac{1}{2} (β - γ) \frac{\sin \frac{1}{2} (b + c)}{\sin \frac{1}{2} (b - c)}] . \end{matrix}$

A side and two adjacent angles given (spherical ASA)

Known: the side Template:Mvar and the angles Template:Mvar. First we determine the angle Template:Mvar using the spherical law of cosines: $γ = \arccos (\sin α \sin β \cos c - \cos α \cos β) .$

We can find the two unknown sides from the spherical law of cosines (using the calculated angle Template:Mvar):

$\begin{matrix} a & = \arccos \frac{\cos α + \cos β \cos γ}{\sin β \sin γ}, \\ b & = \arccos \frac{\cos β + \cos α \cos γ}{\sin α \sin γ}, \end{matrix}$

or by using Napier's analogies: $\begin{matrix} a & = \arctan \frac{2 \sin α}{\cot \frac{1}{2} c \sin (β + α) + \tan \frac{1}{2} c \sin (β - α)}, \\ b & = \arctan \frac{2 \sin β}{\cot \frac{1}{2} c \sin (α + β) + \tan \frac{1}{2} c \sin (α - β)} . \end{matrix}$

File:Solve spherical triangle with a alpha beta.png

A side, one adjacent angle and the opposite angle given (spherical AAS)

Known: the side Template:Mvar and the angles Template:Mvar. The side Template:Mvar can be found from the spherical law of sines: $b = \arcsin \frac{\sin a \sin β}{\sin α} .$

If the angle for the side Template:Math is acute and Template:Math, another solution exists: $b = π - \arcsin \frac{\sin a \sin β}{\sin α} .$

We can find other characteristics by using Napier's analogies: $\begin{matrix} c & = 2 \arctan [\tan \frac{1}{2} (a - b) \frac{\sin \frac{1}{2} (α + β)}{\sin \frac{1}{2} (α - β)}], \\ γ & = 2 arccot [\tan \frac{1}{2} (α - β) \frac{\sin \frac{1}{2} (a + b)}{\sin \frac{1}{2} (a - b)}] . \end{matrix}$

Three angles given (spherical AAA)

Known: the angles Template:Mvar. From the spherical law of cosines we infer: $\begin{matrix} a & = \arccos \frac{\cos α + \cos β \cos γ}{\sin β \sin γ}, \\ b & = \arccos \frac{\cos β + \cos γ \cos α}{\sin γ \sin α}, \\ c & = \arccos \frac{\cos γ + \cos α \cos β}{\sin α \sin β} . \end{matrix}$

Solving right-angled spherical triangles

The above algorithms become much simpler if one of the angles of a triangle (for example, the angle Template:Mvar) is the right angle. Such a spherical triangle is fully defined by its two elements, and the other three can be calculated using Napier's Pentagon or the following relations.

\sin a = \sin c \cdot \sin A

(from the spherical law of sines)

\tan a = \sin b \cdot \tan A

\cos c = \cos a \cdot \cos b

(from the spherical law of cosines)

\tan b = \tan c \cdot \cos A

\cos A = \cos a \cdot \sin B

(also from the spherical law of cosines)

\cos c = \cot A \cdot \cot B

Some applications

Triangulation

Template:Main If one wants to measure the distance Template:Mvar from shore to a remote ship via triangulation, one marks on the shore two points with known distance Template:Mvar between them (the baseline). Let Template:Mvar be the angles between the baseline and the direction to the ship.

From the formulae above (ASA case, assuming planar geometry) one can compute the distance as the triangle height: $d = \frac{\sin α \sin β}{\sin (α + β)} ℓ = \frac{\tan α \tan β}{\tan α + \tan β} ℓ .$

For the spherical case, one can first compute the length of side from the point at Template:Mvar to the ship (i.e. the side opposite to Template:Mvar) via the ASA formula $\tan b = \frac{2 \sin β}{\cot \frac{1}{2} ℓ \sin (α + β) + \tan \frac{1}{2} ℓ \sin (α - β)},$ and insert this into the AAS formula for the right subtriangle that contains the angle Template:Mvar and the sides Template:Mvar and Template:Mvar: $\sin d = \sin b \sin α = \frac{\tan b}{\sqrt{1 + \tan^{2} b}} \sin α .$ (The planar formula is actually the first term of the Taylor expansion of Template:Mvar of the spherical solution in powers of Template:Mvar.)

This method is used in cabotage. The angles Template:Mvar are defined by observation of familiar landmarks from the ship. Template:Clear

As another example, if one wants to measure the height Template:Mvar of a mountain or a high building, the angles Template:Mvar from two ground points to the top are specified. Let Template:Math be the distance between these points. From the same ASA case formulas we obtain: $h = \frac{\sin α \sin β}{\sin (β - α)} ℓ = \frac{\tan α \tan β}{\tan β - \tan α} ℓ .$

The distance between two points on the globe

Template:Main