Hyperbolic functions

In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points Template:Math form a circle with a unit radius, the points Template:Math form the right half of the unit hyperbola. Also, similarly to how the derivatives of Template:Math and Template:Math are Template:Math and Template:Math respectively, the derivatives of Template:Math and Template:Math are Template:Math and Template:Math respectively.

Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics.

The basic hyperbolic functions are:

• hyperbolic sine "Template:Math" (Template:IPAc-en),
• hyperbolic cosine "Template:Math" (Template:IPAc-en),

from which are derived:

• hyperbolic tangent "Template:Math" (Template:IPAc-en),
• hyperbolic cotangent "Template:Math" (Template:IPAc-en),
• hyperbolic secant "Template:Math" (Template:IPAc-en),
• hyperbolic cosecant "Template:Math" or "Template:Math" (Template:IPAc-en)

corresponding to the derived trigonometric functions.

The inverse hyperbolic functions are:

• inverse hyperbolic sine "Template:Math" (also denoted "Template:Math", "Template:Math" or sometimes "Template:Math")
• inverse hyperbolic cosine "Template:Math" (also denoted "Template:Math", "Template:Math" or sometimes "Template:Math")
• inverse hyperbolic tangent "Template:Math" (also denoted "Template:Math", "Template:Math" or sometimes "Template:Math")
• inverse hyperbolic cotangent "Template:Math" (also denoted "Template:Math", "Template:Math" or sometimes "Template:Math")
• inverse hyperbolic secant "Template:Math" (also denoted "Template:Math", "Template:Math" or sometimes "Template:Math")
• inverse hyperbolic cosecant "Template:Math" (also denoted "Template:Math", "Template:Math", "Template:Math","Template:Math", "Template:Math", or sometimes "Template:Math" or "Template:Math")

A ray through the unit hyperbola Template:Math at the point Template:Math, where Template:Mvar is twice the area between the ray, the hyperbola, and the Template:Mvar-axis. For points on the hyperbola below the Template:Mvar-axis, the area is considered negative (see animated version with comparison with the trigonometric (circular) functions).

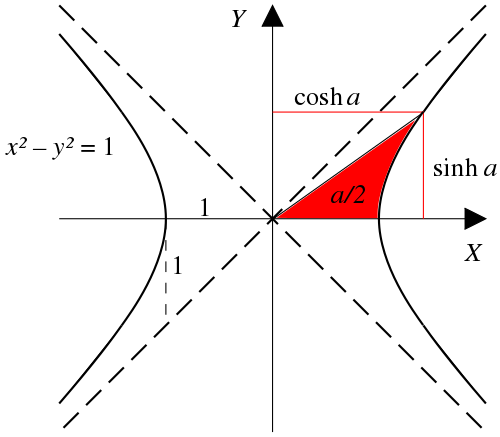
The hyperbolic functions take a real argument called a hyperbolic angle. The magnitude of a hyperbolic angle is the area of its hyperbolic sector to xy = 1. The hyperbolic functions may be defined in terms of the legs of a right triangle covering this sector.

In complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. The hyperbolic sine and the hyperbolic cosine are entire functions. As a result, the other hyperbolic functions are meromorphic in the whole complex plane.

By Lindemann–Weierstrass theorem, the hyperbolic functions have a transcendental value for every non-zero algebraic value of the argument.

Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and Johann Heinrich Lambert. Riccati used Template:Math and Template:Math (Template:Lang) to refer to circular functions and Template:Math and Template:Math (Template:Lang) to refer to hyperbolic functions. Lambert adopted the names, but altered the abbreviations to those used today. The abbreviations Template:Math, Template:Math, Template:Math, Template:Math are also currently used, depending on personal preference.

Definitions

sinh, cosh and tanh

csch, sech and coth

There are various equivalent ways to define the hyperbolic functions.

Exponential definitions

Template:Math is half the difference of Template:Math and Template:Math

Template:Math is the average of Template:Math and Template:Math

In terms of the exponential function:

• Hyperbolic sine: the odd part of the exponential function, that is, $$\sinh x=\frac{e^x-e^{-x}}{2}=\frac{e^{2x}-1}{2e^x}=\frac{1-e^{-2x}}{2e^{-x}}.$$
• Hyperbolic cosine: the even part of the exponential function, that is, $$\cosh x=\frac{e^x+e^{-x}}{2}=\frac{e^{2x}+1}{2e^x}=\frac{1+e^{-2x}}{2e^{-x}}.$$
• Hyperbolic tangent: $$\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}.$$
• Hyperbolic cotangent: for Template:Math, $$\coth x=\frac{\cosh x}{\sinh x}=\frac{e^x+e^{-x}}{e^x-e^{-x}}=\frac{e^{2x}+1}{e^{2x}-1}.$$
• Hyperbolic secant: $$\mathrm{sech}x=\frac{1}{\cosh x}=\frac{2}{e^x+e^{-x}}=\frac{2e^x}{e^{2x}+1}.$$
• Hyperbolic cosecant: for Template:Math, $$\mathrm{csch}x=\frac{1}{\sinh x}=\frac{2}{e^x-e^{-x}}=\frac{2e^x}{e^{2x}-1}.$$

Differential equation definitions

The hyperbolic functions may be defined as solutions of differential equations: The hyperbolic sine and cosine are the solution Template:Math of the system $$\begin{array}{cc}{c}^{\prime }(x)& =s(x),\\ s^{\prime }(x)& =c(x),\\ \end{array}$$ with the initial conditions $s(0)=0,c(0)=1.$ The initial conditions make the solution unique; without them any pair of functions $(a{e}^x+b{e}^{-x},a{e}^x-b{e}^{-x})$ would be a solution.

Template:Math and Template:Math are also the unique solution of the equation Template:Math, such that Template:Math, Template:Math for the hyperbolic cosine, and Template:Math, Template:Math for the hyperbolic sine.

Complex trigonometric definitions

Hyperbolic functions may also be deduced from trigonometric functions with complex arguments:

• Hyperbolic sine: $$\sinh x=-i\sin (ix).$$
• Hyperbolic cosine: $$\cosh x=\cos (ix).$$
• Hyperbolic tangent: $$\tanh x=-i\tan (ix).$$
• Hyperbolic cotangent: $$\coth x=i\cot (ix).$$
• Hyperbolic secant: $$\mathrm{sech}x=\sec (ix).$$
• Hyperbolic cosecant:$$\mathrm{csch}x=i\csc (ix).$$

where Template:Mvar is the imaginary unit with Template:Math.

The above definitions are related to the exponential definitions via Euler's formula (See Template:Section link below).

Characterizing properties

Hyperbolic cosine

It can be shown that the area under the curve of the hyperbolic cosine (over a finite interval) is always equal to the arc length corresponding to that interval: $$\text{area}=\underset{a}{\overset{b}{\int }}\cosh xdx=\underset{a}{\overset{b}{\int }}\sqrt{1+{(\frac{d}{dx}\cosh x)}^2}dx=\text{arc length.}$$

Hyperbolic tangentTemplate:Anchor

The hyperbolic tangent is the (unique) solution to the differential equation Template:Math, with Template:Math.

Useful relations

Template:Anchor The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities. In fact, Osborn's rule states that one can convert any trigonometric identity (up to but not including sinhs or implied sinhs of 4th degree) for $\theta$, $2\theta$, $3\theta$ or $\theta$ and $\phi$ into a hyperbolic identity, by expanding it completely in terms of integral powers of sines and cosines, changing sine to sinh and cosine to cosh, and switching the sign of every term containing a product of two sinhs.

Odd and even functions: $$\begin{array}{cc}\sinh (-x)& =-\sinh x\\ \cosh (-x)& =\cosh x\end{array}$$

Hence: $$\begin{array}{cc}\tanh (-x)& =-\tanh x\\ \coth (-x)& =-\coth x\\ \mathrm{sech}(-x)& =\mathrm{sech}x\\ \mathrm{csch}(-x)& =-\mathrm{csch}x\end{array}$$

Thus, Template:Math and Template:Math are even functions; the others are odd functions.

$$\begin{array}{cc}\mathrm{arsech}x& =\mathrm{arcosh}\left(\frac{1}{x}\right)\\ \mathrm{arcsch}x& =\mathrm{arsinh}\left(\frac{1}{x}\right)\\ \mathrm{arcoth}x& =\mathrm{artanh}\left(\frac{1}{x}\right)\end{array}$$

Hyperbolic sine and cosine satisfy: $$\begin{array}{cc}\cosh x+\sinh x& =e^x\\ \cosh x-\sinh x& =e^{-x}\end{array}$$

which are analogous to Euler's formula, and

$${\cosh }^{2}x-{\sinh }^{2}x=1$$

which is analogous to the Pythagorean trigonometric identity.

One also has $$\begin{array}{cc}{\mathrm{sech}}^{2}x& =1-{\tanh }^{2}x\\ {\mathrm{csch}}^{2}x& ={\coth }^{2}x-1\end{array}$$

for the other functions.

Sums of arguments

$$\begin{array}{cc}\sinh (x+y)& =\sinh x\cosh y+\cosh x\sinh y\\ \cosh (x+y)& =\cosh x\cosh y+\sinh x\sinh y\\ \tanh (x+y)& =\frac{\tanh x+\tanh y}{1+\tanh x\tanh y}\\ \end{array}$$ particularly $$\begin{array}{cc}\cosh (2x)& ={\sinh }^{2}x+{\cosh }^{2}x=2{\sinh }^{2}x+1=2{\cosh }^{2}x-1\\ \sinh (2x)& =2\sinh x\cosh x\\ \tanh (2x)& =\frac{2\tanh x}{1+{\tanh }^{2}x}\\ \end{array}$$

Also: $$\begin{array}{cc}\sinh x+\sinh y& =2\sinh \left(\frac{x+y}{2}\right)\cosh \left(\frac{x-y}{2}\right)\\ \cosh x+\cosh y& =2\cosh \left(\frac{x+y}{2}\right)\cosh \left(\frac{x-y}{2}\right)\\ \end{array}$$

Subtraction formulas

$$\begin{array}{cc}\sinh (x-y)& =\sinh x\cosh y-\cosh x\sinh y\\ \cosh (x-y)& =\cosh x\cosh y-\sinh x\sinh y\\ \tanh (x-y)& =\frac{\tanh x-\tanh y}{1-\tanh x\tanh y}\\ \end{array}$$

Also: $$\begin{array}{cc}\sinh x-\sinh y& =2\cosh \left(\frac{x+y}{2}\right)\sinh \left(\frac{x-y}{2}\right)\\ \cosh x-\cosh y& =2\sinh \left(\frac{x+y}{2}\right)\sinh \left(\frac{x-y}{2}\right)\\ \end{array}$$

Half argument formulas

$$\begin{array}{cccc}\sinh \left(\frac{x}{2}\right)& =\frac{\sinh x}{\sqrt{2(\cosh x+1)}}& & =\mathrm{sgn}x\sqrt{\frac{\cosh x-1}{2}}\\ [6px]\cosh \left(\frac{x}{2}\right)& =\sqrt{\frac{\cosh x+1}{2}}\\ [6px]\tanh \left(\frac{x}{2}\right)& =\frac{\sinh x}{\cosh x+1}& & =\mathrm{sgn}x\sqrt{\frac{\cosh x-1}{\cosh x+1}}=\frac{e^x-1}{e^x+1}\end{array}$$

where Template:Math is the sign function.

If Template:Math, then

$$\tanh \left(\frac{x}{2}\right)=\frac{\cosh x-1}{\sinh x}=\coth x-\mathrm{csch}x$$

Square formulas

$$\begin{array}{cc}{\sinh }^{2}x& =\frac{1}{2}(\cosh 2x-1)\\ {\cosh }^{2}x& =\frac{1}{2}(\cosh 2x+1)\end{array}$$

Inequalities

The following inequality is useful in statistics: $$\cosh (t)\le e^{t^2/2}.$$

It can be proved by comparing the Taylor series of the two functions term by term.

Inverse functions as logarithms

$$\begin{array}{cc}\mathrm{arsinh}(x)& =\ln (x+\sqrt{x^2+1})\\ \mathrm{arcosh}(x)& =\ln (x+\sqrt{x^2-1})& & x\ge 1\\ \mathrm{artanh}(x)& =\frac{1}{2}\ln \left(\frac{1+x}{1-x}\right)& & |x|<1\\ \mathrm{arcoth}(x)& =\frac{1}{2}\ln \left(\frac{x+1}{x-1}\right)& & |x|>1\\ \mathrm{arsech}(x)& =\ln (\frac{1}{x}+\sqrt{\frac{1}{x^2}-1})=\ln \left(\frac{1+\sqrt{1-x^2}}{x}\right)& & 0<x\le 1\\ \mathrm{arcsch}(x)& =\ln (\frac{1}{x}+\sqrt{\frac{1}{x^2}+1})& & x\ne 0\end{array}$$

Derivatives

$$\begin{array}{cc}\frac{d}{dx}\sinh x& =\cosh x\\ \frac{d}{dx}\cosh x& =\sinh x\\ \frac{d}{dx}\tanh x& =1-{\tanh }^{2}x={\mathrm{sech}}^{2}x=\frac{1}{{\cosh }^{2}x}\\ \frac{d}{dx}\coth x& =1-{\coth }^{2}x=-{\mathrm{csch}}^{2}x=-\frac{1}{{\sinh }^{2}x}& & x\ne 0\\ \frac{d}{dx}\mathrm{sech}x& =-\tanh x\mathrm{sech}x\\ \frac{d}{dx}\mathrm{csch}x& =-\coth x\mathrm{csch}x& & x\ne 0\end{array}$$ $$\begin{array}{cc}\frac{d}{dx}\mathrm{arsinh}x& =\frac{1}{\sqrt{x^2+1}}\\ \frac{d}{dx}\mathrm{arcosh}x& =\frac{1}{\sqrt{x^2-1}}& & 1<x\\ \frac{d}{dx}\mathrm{artanh}x& =\frac{1}{1-x^2}& & |x|<1\\ \frac{d}{dx}\mathrm{arcoth}x& =\frac{1}{1-x^2}& & 1<|x|\\ \frac{d}{dx}\mathrm{arsech}x& =-\frac{1}{x\sqrt{1-x^2}}& & 0<x<1\\ \frac{d}{dx}\mathrm{arcsch}x& =-\frac{1}{|x|\sqrt{1+x^2}}& & x\ne 0\end{array}$$

Second derivatives

Each of the functions Template:Math and Template:Math is equal to its second derivative, that is: $$\frac{d^2}{d{x}^2}\sinh x=\sinh x$$ $$\frac{d^2}{d{x}^2}\cosh x=\cosh x.$$

All functions with this property are linear combinations of Template:Math and Template:Math, in particular the exponential functions $e^x$ and $e^{-x}$.

Standard integrals

$$\begin{array}{cc}\int \sinh (ax)dx& =a^{-1}\cosh (ax)+C\\ \int \cosh (ax)dx& =a^{-1}\sinh (ax)+C\\ \int \tanh (ax)dx& =a^{-1}\ln (\cosh (ax))+C\\ \int \coth (ax)dx& =a^{-1}\ln |\sinh (ax)|+C\\ \int \mathrm{sech}(ax)dx& =a^{-1}\arctan (\sinh (ax))+C\\ \int \mathrm{csch}(ax)dx& =a^{-1}\ln |\tanh \left(\frac{ax}{2}\right)|+C=a^{-1}\ln |\coth \left(ax\right)-\mathrm{csch}\left(ax\right)|+C=-a^{-1}\mathrm{arcoth}(\cosh \left(ax\right))+C\end{array}$$

The following integrals can be proved using hyperbolic substitution: $$\begin{array}{cc}\int \frac{1}{\sqrt{a^2+u^2}}du& =\mathrm{arsinh}\left(\frac{u}{a}\right)+C\\ \int \frac{1}{\sqrt{u^2-a^2}}du& =\mathrm{sgn}u\mathrm{arcosh}\left|\frac{u}{a}\right|+C\\ \int \frac{1}{a^2-u^2}du& =a^{-1}\mathrm{artanh}\left(\frac{u}{a}\right)+C& & u^2<a^2\\ \int \frac{1}{a^2-u^2}du& =a^{-1}\mathrm{arcoth}\left(\frac{u}{a}\right)+C& & u^2>a^2\\ \int \frac{1}{u\sqrt{a^2-u^2}}du& =-a^{-1}\mathrm{arsech}\left|\frac{u}{a}\right|+C\\ \int \frac{1}{u\sqrt{a^2+u^2}}du& =-a^{-1}\mathrm{arcsch}\left|\frac{u}{a}\right|+C\end{array}$$

where C is the constant of integration.

Taylor series expressions

It is possible to express explicitly the Taylor series at zero (or the Laurent series, if the function is not defined at zero) of the above functions.

$$\sinh x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{x^{2n+1}}{(2n+1)!}$$ This series is convergent for every complex value of Template:Mvar. Since the function Template:Math is odd, only odd exponents for Template:Math occur in its Taylor series.

$$\cosh x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{x^{2n}}{(2n)!}$$ This series is convergent for every complex value of Template:Mvar. Since the function Template:Math is even, only even exponents for Template:Mvar occur in its Taylor series.

The sum of the sinh and cosh series is the infinite series expression of the exponential function.

The following series are followed by a description of a subset of their domain of convergence, where the series is convergent and its sum equals the function. $$\begin{array}{cc}\tanh x& =x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum _{n=1}^{\mathrm{\infty }}\frac{2^{2n}(2^{2n}-1)B_{2n}{x}^{2n-1}}{(2n)!},\left|x\right|<\frac{\pi }{2}\\ \coth x& =x^{-1}+\frac{x}{3}-\frac{x^3}{45}+\frac{2x^5}{945}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{2^{2n}{B}_{2n}{x}^{2n-1}}{(2n)!},0<\left|x\right|<\pi \\ \mathrm{sech}x& =1-\frac{x^2}{2}+\frac{5x^4}{24}-\frac{61x^6}{720}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{E_{2n}{x}^{2n}}{(2n)!},\left|x\right|<\frac{\pi }{2}\\ \mathrm{csch}x& =x^{-1}-\frac{x}{6}+\frac{7x^3}{360}-\frac{31x^5}{15120}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{2(1-2^{2n-1})B_{2n}{x}^{2n-1}}{(2n)!},0<\left|x\right|<\pi \end{array}$$

where:

• $B_n$ is the nth Bernoulli number
• $E_n$ is the nth Euler number

Infinite products and continued fractions

The following expansions are valid in the whole complex plane:

$\sinh x=x\prod _{n=1}^{\mathrm{\infty }}(1+\frac{x^2}{n^2{\pi }^2})=\frac{x}{1-\frac{x^2}{2\cdot 3+x^2-\frac{2\cdot 3x^2}{4\cdot 5+x^2-\frac{4\cdot 5x^2}{6\cdot 7+x^2-\ddots }}}}$

$\cosh x=\prod _{n=1}^{\mathrm{\infty }}(1+\frac{x^2}{(n-1/2{)}^2{\pi }^2})=\frac{1}{1-\frac{x^2}{1\cdot 2+x^2-\frac{1\cdot 2x^2}{3\cdot 4+x^2-\frac{3\cdot 4x^2}{5\cdot 6+x^2-\ddots }}}}$

$\tanh x=\frac{1}{\frac{1}{x}+\frac{1}{\frac{3}{x}+\frac{1}{\frac{5}{x}+\frac{1}{\frac{7}{x}+\ddots }}}}$

Comparison with circular functions

Circle and hyperbola tangent at (1,1) display geometry of circular functions in terms of circular sector area Template:Mvar and hyperbolic functions depending on hyperbolic sector area Template:Mvar.

The hyperbolic functions represent an expansion of trigonometry beyond the circular functions. Both types depend on an argument, either circular angle or hyperbolic angle.

Since the area of a circular sector with radius Template:Mvar and angle Template:Mvar (in radians) is Template:Math, it will be equal to Template:Mvar when Template:Math. In the diagram, such a circle is tangent to the hyperbola xy = 1 at (1,1). The yellow sector depicts an area and angle magnitude. Similarly, the yellow and red regions together depict a hyperbolic sector with area corresponding to hyperbolic angle magnitude.

The legs of the two right triangles with hypotenuse on the ray defining the angles are of length Template:Radic times the circular and hyperbolic functions.

The hyperbolic angle is an invariant measure with respect to the squeeze mapping, just as the circular angle is invariant under rotation.

The Gudermannian function gives a direct relationship between the circular functions and the hyperbolic functions that does not involve complex numbers.

The graph of the function Template:Math is the catenary, the curve formed by a uniform flexible chain, hanging freely between two fixed points under uniform gravity.

Relationship to the exponential function

The decomposition of the exponential function in its even and odd parts gives the identities $$e^x=\cosh x+\sinh x,$$ and $$e^{-x}=\cosh x-\sinh x.$$ Combined with Euler's formula $$e^{ix}=\cos x+i\sin x,$$ this gives $$e^{x+iy}=(\cosh x+\sinh x)(\cos y+i\sin y)$$ for the general complex exponential function.

Additionally, $$e^x=\sqrt{\frac{1+\tanh x}{1-\tanh x}}=\frac{1+\tanh \frac{x}{2}}{1-\tanh \frac{x}{2}}$$

Hyperbolic functions for complex numbers

Hyperbolic functions in the complex plane

$\sinh (z)$	$\cosh (z)$	$\tanh (z)$	$\coth (z)$	$\mathrm{sech}(z)$	$\mathrm{csch}(z)$

Since the exponential function can be defined for any complex argument, we can also extend the definitions of the hyperbolic functions to complex arguments. The functions Template:Math and Template:Math are then holomorphic.

Relationships to ordinary trigonometric functions are given by Euler's formula for complex numbers: $$\begin{array}{cc}{e}^{ix}& =\cos x+i\sin x\\ e^{-ix}& =\cos x-i\sin x\end{array}$$ so: $$\begin{array}{cc}\cosh (ix)& =\frac{1}{2}(e^{ix}+e^{-ix})=\cos x\\ \sinh (ix)& =\frac{1}{2}(e^{ix}-e^{-ix})=i\sin x\\ \cosh (x+iy)& =\cosh (x)\cos (y)+i\sinh (x)\sin (y)\\ \sinh (x+iy)& =\sinh (x)\cos (y)+i\cosh (x)\sin (y)\\ \tanh (ix)& =i\tan x\\ \cosh x& =\cos (ix)\\ \sinh x& =-i\sin (ix)\\ \tanh x& =-i\tan (ix)\end{array}$$

Thus, hyperbolic functions are periodic with respect to the imaginary component, with period $2\pi i$ ($\pi i$ for hyperbolic tangent and cotangent).

See also

• e (mathematical constant)
• Equal incircles theorem, based on sinh
• Hyperbolastic functions
• Hyperbolic growth
• Inverse hyperbolic functions
• List of integrals of hyperbolic functions
• Poinsot's spirals
• Sigmoid function
• Soboleva modified hyperbolic tangent
• Trigonometric functions

External links

• Template:Springer
• Hyperbolic functions on PlanetMath
• GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions (Java Web Start)
• Web-based calculator of hyperbolic functions