Great truncated cuboctahedron

Template:Short description Template:Uniform polyhedra db File:Great truncated cuboctahedron.stl In geometry, the great truncated cuboctahedron (or quasitruncated cuboctahedron or stellatruncated cuboctahedron) is a nonconvex uniform polyhedron, indexed as U₂₀. It has 26 faces (12 squares, 8 hexagons and 6 octagrams), 72 edges, and 48 vertices. It is represented by the Schläfli symbol tr{⁴/₃,3}, and Coxeter-Dynkin diagram Template:CDD. It is sometimes called the quasitruncated cuboctahedron because it is related to the truncated cuboctahedron, Template:CDD, except that the octagonal faces are replaced by {⁸/₃} octagrams.

Convex hull

Its convex hull is a nonuniform truncated cuboctahedron. The truncated cuboctahedron and the great truncated cuboctahedron form isomorphic graphs despite their different geometric structure.

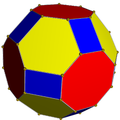Convex hull

Great truncated cuboctahedron

Orthographic projections

Cartesian coordinates

Cartesian coordinates for the vertices of a great truncated cuboctahedron centered at the origin are all permutations of $$(\pm 1,\pm [1-\sqrt{2}],\pm [1-2\sqrt{2}]).$$

See also

• List of uniform polyhedra

External links

• Template:Mathworld

Template:Polyhedron-stub