Antiprism

Octagonal antiprism

Template:More footnotes In geometry, an Template:Nowrap antiprism or Template:Nowrap is a polyhedron composed of two parallel direct copies (not mirror images) of an Template:Nowrap polygon, connected by an alternating band of Template:Math triangles. They are represented by the Conway notation Template:Math.

Antiprisms are a subclass of prismatoids, and are a (degenerate) type of snub polyhedron.

Antiprisms are similar to prisms, except that the bases are twisted relatively to each other, and that the side faces (connecting the bases) are Template:Math triangles, rather than Template:Mvar quadrilaterals.

The dual polyhedron of an Template:Mvar-gonal antiprism is an Template:Mvar-gonal trapezohedron.

History

In his 1619 book Harmonices Mundi, Johannes Kepler observed the existence of the infinite family of antiprisms. This has conventionally been thought of as the first discovery of these shapes, but they may have been known earlier: an unsigned printing block for the net of a hexagonal antiprism has been attributed to Hieronymus Andreae, who died in 1556.

The German form of the word "antiprism" was used for these shapes in the 19th century; Karl Heinze credits its introduction to Template:Ill. Although the English "anti-prism" had been used earlier for an optical prism used to cancel the effects of a primary optical element, the first use of "antiprism" in English in its geometric sense appears to be in the early 20th century in the works of H. S. M. Coxeter.

Special cases

Right antiprism

For an antiprism with [[Regular polygon|regular Template:Mvar-gon]] bases, one usually considers the case where these two copies are twisted by an angle of Template:Math degrees.

The axis of a regular polygon is the line perpendicular to the polygon plane and lying in the polygon centre.

For an antiprism with congruent regular Template:Mvar-gon bases, twisted by an angle of Template:Math degrees, more regularity is obtained if the bases have the same axis: are coaxial; i.e. (for non-coplanar bases): if the line connecting the base centers is perpendicular to the base planes. Then the antiprism is called a right antiprism, and its Template:Math side faces are isosceles triangles.

Uniform antiprism

A uniform Template:Mvar-antiprism has two congruent regular Template:Mvar-gons as base faces, and Template:Math equilateral triangles as side faces.

Uniform antiprisms form an infinite class of vertex-transitive polyhedra, as do uniform prisms. For Template:Math, we have the digonal antiprism (degenerate antiprism), which is visually identical to the regular tetrahedron; for Template:Math, the regular octahedron as a triangular antiprism (non-degenerate antiprism).

The Schlegel diagrams of these semiregular antiprisms are as follows:

A3

A4

A5

A6

A7

A8

Cartesian coordinates

Cartesian coordinates for the vertices of a right Template:Mvar-antiprism (i.e. with regular Template:Mvar-gon bases and Template:Math isosceles triangle side faces, circumradius of the bases equal to 1) are:

$(\cos \frac{k\pi }{n},\sin \frac{k\pi }{n},(-1{)}^{k}h)$

where Template:Math;

if the Template:Mvar-antiprism is uniform (i.e. if the triangles are equilateral), then: $$2h^2=\cos \frac{\pi }{n}-\cos \frac{2\pi }{n}.$$

Volume and surface area

Let Template:Mvar be the edge-length of a uniform Template:Mvar-gonal antiprism; then the volume is: $$V=\frac{n\sqrt{4{\cos }^2\frac{\pi }{2n}-1}\sin \frac{3\pi }{2n}}{12{\sin }^2\frac{\pi }{n}}{a}^3,$$

and the surface area is: $$A=\frac{n}{2}(\cot \frac{\pi }{n}+\sqrt{3})a^2.$$

Furthermore, the volume of a regular [[Antiprism#Right_antiprism|right Template:Mvar-gonal antiprism]] with side length of its bases Template:Mvar and height Template:Mvar is given by: $$V=\frac{nh{l}^2}{12}(\csc \frac{\pi }{n}+2\cot \frac{\pi }{n}).$$

Derivation

The circumradius of the horizontal circumcircle of the regular $n$-gon at the base is

$R(0)=\frac{l}{2\sin \frac{\pi }{n}}.$

The vertices at the base are at

$\left(\begin{array}{c}R(0)\cos \frac{2\pi m}{n}\\ R(0)\sin \frac{2\pi m}{n}\\ 0\end{array}\right),m=0..n-1;$

the vertices at the top are at

$\left(\begin{array}{c}R(0)\cos \frac{2\pi (m+1/2)}{n}\\ R(0)\sin \frac{2\pi (m+1/2)}{n}\\ h\end{array}\right),m=0..n-1.$

Via linear interpolation, points on the outer triangular edges of the antiprism that connect vertices at the bottom with vertices at the top are at

$\left(\begin{array}{c}\frac{R(0)}{h}[(h-z)\cos \frac{2\pi m}{n}+z\cos \frac{\pi (2m+1)}{n}]\\ \frac{R(0)}{h}[(h-z)\sin \frac{2\pi m}{n}+z\sin \frac{\pi (2m+1)}{n}]\\ \\ z\end{array}\right),0\le z\le h,m=0..n-1$

and at

$\left(\begin{array}{c}\frac{R(0)}{h}[(h-z)\cos \frac{2\pi (m+1)}{n}+z\cos \frac{\pi (2m+1)}{n}]\\ \frac{R(0)}{h}[(h-z)\sin \frac{2\pi (m+1)}{n}+z\sin \frac{\pi (2m+1)}{n}]\\ \\ z\end{array}\right),0\le z\le h,m=0..n-1.$

By building the sums of the squares of the $x$ and $y$ coordinates in one of the previous two vectors, the squared circumradius of this section at altitude $z$ is

$R(z{)}^2=\frac{R(0{)}^2}{h^2}[h^2-2hz+2z^2+2z(h-z)\cos \frac{\pi }{n}].$

The horizontal section at altitude $0\le z\le h$ above the base is a $2n$-gon (truncated $n$-gon) with $n$ sides of length $l_1(z)=l(1-z/h)$ alternating with $n$ sides of length $l_2(z)=lz/h$. (These are derived from the length of the difference of the previous two vectors.) It can be dissected into $n$ isoceless triangles of edges $R(z),R(z)$ and $l_1$ (semiperimeter $R(z)+l_1(z)/2$) plus $n$ isoceless triangles of edges $R(z),R(z)$ and $l_2(z)$ (semiperimeter $R(z)+l_2(z)/2$). According to Heron's formula the areas of these triangles are

$Q_1(z)=\frac{R(0{)}^2}{h^2}(h-z)[(h-z)\cos \frac{\pi }{n}+z]\sin \frac{\pi }{n}$

and

$Q_2(z)=\frac{R(0{)}^2}{h^2}z[z\cos \frac{\pi }{n}+h-z]\sin \frac{\pi }{n}.$

The area of the section is $n[Q_1(z)+Q_2(z)]$, and the volume is

$V=n\underset{0}{\overset{h}{\int }}[Q_1(z)+Q_2(z)]dz=\frac{nh}{3}R(0{)}^2\sin \frac{\pi }{n}(1+2\cos \frac{\pi }{n})=\frac{nh}{12}{l}^2\frac{1+2\cos \frac{\pi }{n}}{\sin \frac{\pi }{n}}.$

Note that the volume of a right Template:Mvar-gonal prism with the same Template:Mvar and Template:Mvar is: $$V_{\mathrm{p}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{m}}=\frac{nh{l}^2}{4}\cot \frac{\pi }{n}$$ which is smaller than that of an antiprism.

Symmetry

The symmetry group of a right Template:Mvar-antiprism (i.e. with regular bases and isosceles side faces) is Template:Math of order Template:Math, except in the cases of:

• Template:Math: the regular tetrahedron, which has the larger symmetry group Template:Math of order Template:Math, which has three versions of Template:Math as subgroups;

• Template:Math: the regular octahedron, which has the larger symmetry group Template:Math of order Template:Math, which has four versions of Template:Math as subgroups.

The symmetry group contains inversion if and only if Template:Mvar is odd.

The rotation group is Template:Math of order Template:Math, except in the cases of:

• Template:Math: the regular tetrahedron, which has the larger rotation group Template:Math of order Template:Math, which has three versions of Template:Math as subgroups;

• Template:Math: the regular octahedron, which has the larger rotation group Template:Math of order Template:Math, which has four versions of Template:Math as subgroups.

Note: The right Template:Mvar-antiprisms have congruent regular Template:Mvar-gon bases and congruent isosceles triangle side faces, thus have the same (dihedral) symmetry group as the uniform Template:Mvar-antiprism, for Template:Math.

Generalizations

In higher dimensions

Four-dimensional antiprisms can be defined as having two dual polyhedra as parallel opposite faces, so that each three-dimensional face between them comes from two dual parts of the polyhedra: a vertex and a dual polygon, or two dual edges. Every three-dimensional convex polyhedron is combinatorially equivalent to one of the two opposite faces of a four-dimensional antiprism, constructed from its canonical polyhedron and its polar dual. However, there exist four-dimensional polychora that cannot be combined with their duals to form five-dimensional antiprisms.

Self-crossing polyhedra

3/2-antiprism nonuniform	5/4-antiprism nonuniform	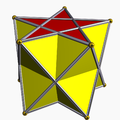5/2-antiprism	5/3-antiprism
9/2-antiprism	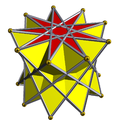9/4-antiprism	9/5-antiprism

This shows all the non-star and star antiprisms up to 15 sides, together with those of a 29-agon.

Uniform star antiprisms are named by their star polygon bases, Template:Math and exist in prograde and in retrograde (crossed) solutions. Crossed forms have intersecting vertex figures, and are denoted by "inverted" fractions: Template:Math instead of Template:Math; example: 5/3 instead of 5/2.

A right star antiprism has two congruent coaxial regular convex or star polygon base faces, and Template:Math isosceles triangle side faces.

Any star antiprism with regular convex or star polygon bases can be made a right star antiprism (by translating and/or twisting one of its bases, if necessary).

In the retrograde forms, but not in the prograde forms, the triangles joining the convex or star bases intersect the axis of rotational symmetry. Thus:

• Retrograde star antiprisms with regular convex polygon bases cannot have all equal edge lengths, and so cannot be uniform. "Exception": a retrograde star antiprism with equilateral triangle bases (vertex configuration: 3.3/2.3.3) can be uniform; but then, it has the appearance of an equilateral triangle: it is a degenerate star polyhedron.

• Similarly, some retrograde star antiprisms with regular star polygon bases cannot have all equal edge lengths, and so cannot be uniform. Example: a retrograde star antiprism with regular star 7/5-gon bases (vertex configuration: 3.3.3.7/5) cannot be uniform.

Also, star antiprism compounds with regular star Template:Math-gon bases can be constructed if Template:Mvar and Template:Mvar have common factors. Example: a star 10/4-antiprism is the compound of two star 5/2-antiprisms.

Star Template:Math-antiprisms by symmetry, for Template:Math

Symmetry group	Uniform stars				Right stars
Template:Math					3.3/2.3.4 Crossed square antiprism
Template:Math	3.3.3.5/2 Pentagrammic antiprism				3.3/2.3.5 crossed pentagonal antiprism
Template:Math	3.3.3.5/3 Pentagrammic crossed-antiprism
Template:Math					3.3/2.3.6 crossed hexagonal antiprism
Template:Math	3.3.3.7/2	3.3.3.7/4
Template:Math	3.3.3.7/3
Template:Math	3.3.3.8/3 Octagrammic antiprism	3.3.3.8/5 Octagrammic crossed-antiprism
Template:Math	3.3.3.9/2 Enneagrammic antiprism (9/2)	3.3.3.9/4 Enneagrammic antiprism (9/4)
Template:Math	3.3.3.9/5 Enneagrammic crossed-antiprism
Template:Math	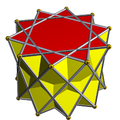3.3.3.10/3 Decagrammic antiprism
Template:Math	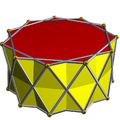3.3.3.11/2	3.3.3.11/4	3.3.3.11/6
Template:Math	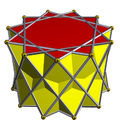3.3.3.11/3	3.3.3.11/5	3.3.3.11/7
Template:Math	3.3.3.12/5	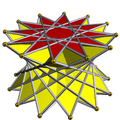3.3.3.12/7
...	...

See also

• Grand antiprism, a four-dimensional polytope
• Skew polygon, a three-dimensional polygon whose convex hull is an antiprism

Further reading

• Template:Cite book Chapter 2: Archimedean polyhedra, prisms and antiprisms

External links

• Template:Commonscatinline
• Template:MathWorld
• Nonconvex Prisms and Antiprisms
• Paper models of prisms and antiprisms