List of quantum logic gates: Difference between revisions
imported>Countercheck light copyedit |
(No difference)
|
Latest revision as of 22:01, 22 February 2025
In gate-based quantum computing, various sets of quantum logic gates are commonly used to express quantum operations. The following tables list several unitary quantum logic gates, together with their common name, how they are represented, and some of their properties. Controlled or conjugate transpose (adjoint) versions of some of these gates may not be listed.
Identity gate and global phase
| Name | # qubits | Operator symbol | Matrix | Circuit diagram | Properties | Refs |
|---|---|---|---|---|---|---|
| Identity,
no-op |
1 (any) | , Template:Not a typo |  or |
[1] | ||
| Global phase | 1 (any) | , or |
|
[1] |
The identity gate is the identity operation , most of the times this gate is not indicated in circuit diagrams, but it is useful when describing mathematical results.
It has been described as being a "wait cycle",[2] and a NOP.[3][1]
The global phase gate introduces a global phase to the whole qubit quantum state. A quantum state is uniquely defined up to a phase. Because of the Born rule, a phase factor has no effect on a measurement outcome: for any .
Because when the global phase gate is applied to a single qubit in a quantum register, the entire register's global phase is changed.
Also,
These gates can be extended to any number of qubits or qudits.
Clifford qubit gates
This table includes commonly used Clifford gates for qubits.[1][4][5]
| Names | # qubits | Operator symbol | Matrix | Circuit diagram | Some properties | Refs |
|---|---|---|---|---|---|---|
| Pauli X, NOT, bit flip |
1 |
|
[1][6] | |||
| Pauli Y | 1 | 
|
|
[1][6] | ||
| Pauli Z, phase flip |
1 | 
|
|
[1][6] | ||
| Phase gate S, square root of Z |
1 | 
|
[1][6] | |||
| Square root of X, square root of NOT |
1 | , , | 
|
[1][7] | ||
| Hadamard, Walsh-Hadamard |
1 | 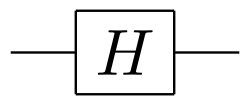
|
|
[1][6] | ||
| Controlled NOT, controlled-X, controlled-bit flip, reversible exclusive OR, Feynman |
2 | , |  |
Implementation: |
[1][6] | |
| Anticontrolled-NOT, anticontrolled-X, zero control, control-on-0-NOT, reversible exclusive NOR |
2 | , , | 
|
|
[1] | |
| Controlled-Z, controlled sign flip, controlled phase flip |
2 | , , , | 
|
Implementation:
|
[1][6] | |
| Double-controlled NOT | 2 | 
|
[8] | |||
| Swap | 2 |  or 
|
|
[1][6] | ||
| Imaginary swap | 2 |  or 
|
|
[1] |
Other Clifford gates, including higher dimensional ones are not included here but by definition can be generated using and .
Note that if a Clifford gate A is not in the Pauli group, or controlled-A are not in the Clifford gates.Template:Citation needed
The Clifford set is not a universal quantum gate set.
Non-Clifford qubit gates
Relative phase gates
| Names | # qubits | Operator symbol | Matrix | Circuit diagram | Properties | Refs |
|---|---|---|---|---|---|---|
| Phase shift | 1 | 
|
|
[9][10][11] | ||
| Phase gate T, π/8 gate, fourth root of Z |
1 | or | 
|
[1][6] | ||
| Controlled phase | 2 | 
|
Implementation:
|
[11] | ||
| Controlled phase S | 2 | 
|
|
[6] |
The phase shift is a family of single-qubit gates that map the basis states and . The probability of measuring a or is unchanged after applying this gate, however it modifies the phase of the quantum state. This is equivalent to tracing a horizontal circle (a line of latitude), or a rotation along the z-axis on the Bloch sphere by radians. A common example is the T gate where (historically known as the gate), the phase gate. Note that some Clifford gates are special cases of the phase shift gate:
The argument to the phase shift gate is in U(1), and the gate performs a phase rotation in U(1) along the specified basis state (e.g. rotates the phase about Template:Nowrap. Extending to a rotation about a generic phase of both basis states of a 2-level quantum system (a qubit) can be done with a series circuit: . When this gate is the rotation operator gate and if it is a global phase.Template:EfnTemplate:Efn
The T gate's historic name of gate comes from the identity , where .
Arbitrary single-qubit phase shift gates are natively available for transmon quantum processors through timing of microwave control pulses.[13] It can be explained in terms of change of frame.[14][15]
As with any single qubit gate one can build a controlled version of the phase shift gate. With respect to the computational basis, the 2-qubit controlled phase shift gate is: shifts the phase with only if it acts on the state :
The controlled-Z (or CZ) gate is the special case where .
The controlled-S gate is the case of the controlled- when and is a commonly used gate.[6]
Rotation operator gates
| Names | # qubits | Operator symbol | Exponential form | Matrix | Circuit diagram | Properties | Refs |
|---|---|---|---|---|---|---|---|
| Rotation about x-axis | 1 |
|
[1][6] | ||||
| Rotation about y-axis | 1 |
|
[1][6] | ||||
| Rotation about z-axis | 1 |
|
[1][6] |
The rotation operator gates and are the analog rotation matrices in three Cartesian axes of SO(3),Template:Efn along the x, y or z-axes of the Bloch sphere projection.
As Pauli matrices are related to the generator of rotations, these rotation operators can be written as matrix exponentials with Pauli matrices in the argument. Any unitary matrix in SU(2) can be written as a product (i.e. series circuit) of three rotation gates or less. Note that for two-level systems such as qubits and spinors, these rotations have a period of Template:Math. A rotation of Template:Math (360 degrees) returns the same statevector with a different phase.[16]
We also have and for all
The rotation matrices are related to the Pauli matrices in the following way:
It is possible to work out the adjoint action of rotations on the Pauli vector, namely rotation effectively by double the angle Template:Mvar to apply Rodrigues' rotation formula:
Taking the dot product of any unit vector with the above formula generates the expression of any single qubit gate when sandwiched within adjoint rotation gates. For example, it can be shown that . Also, using the anticommuting relation we have .
Rotation operators have interesting identities. For example, and Also, using the anticommuting relations we have and
Global phase and phase shift can be transformed into each other's with the Z-rotation operator: .Template:RTemplate:R
The gate represents a rotation of Template:Math about the x axis at the Bloch sphere .
Similar rotation operator gates exist for SU(3) using Gell-Mann matrices. They are the rotation operators used with qutrits.
Two-qubit interaction gates
| Names | # qubits | Operator symbol | Exponential form | Matrix | Circuit diagram | Properties | Refs |
|---|---|---|---|---|---|---|---|
| XX interaction | 2 | , |
Implementation: |
Template:Citation needed | |||
| YY interaction | 2 | , |
Implementation: |
Template:Citation needed | |||
| ZZ interaction | 2 | , |
|
Template:Citation needed | |||
| XY, XX plus YY |
2 | , |
|
Template:Citation needed |
The qubit-qubit Ising coupling or Heisenberg interaction gates Rxx, Ryy and Rzz are 2-qubit gates that are implemented natively in some trapped-ion quantum computers, using for example the Mølmer–Sørensen gate procedure.[17][18]
Note that these gates can be expressed in sinusoidal form also, for example .
The CNOT gate can be further decomposed as products of rotation operator gates and exactly a single two-qubit interaction gate, for example
The SWAP gate can be constructed from other gates, for example using the two-qubit interaction gates: .
In superconducting circuits, the family of gates resulting from Heisenberg interactions is sometimes called the fSim gate set. They can be realized using flux-tunable qubits with flux-tunable coupling,[19] or using microwave drives in fixed-frequency qubits with fixed coupling.[20]
Non-Clifford swap gates
| Names | # qubits | Operator symbol | Matrix | Circuit diagram | Properties | Refs |
|---|---|---|---|---|---|---|
| Square root swap | 2 | 
|
[1] | |||
| Square root imaginary swap | 2 |
|
[11] | |||
| Swap (raised to a power) | 2 | 
|
|
[1] | ||
| Fredkin,
controlled swap |
3 | , |  or 
|
|
[1][6] |
The Template:Radic gate performs half-way of a two-qubit swap (see Clifford gates). It is universal such that any many-qubit gate can be constructed from only Template:Radic and single qubit gates. More than one application of the Template:Radic is required to produce a Bell state from product states. The Template:Radic gate arises naturally in systems that exploit exchange interaction.[21][1]
For systems with Ising like interactions, it is sometimes more natural to introduce the imaginary swap[22] or iSWAP.[23][24] Note that and , or more generally for all real n except 0.
SWAPα arises naturally in spintronic quantum computers.[1]
The Fredkin gate (also CSWAP or CS gate), named after Edward Fredkin, is a 3-bit gate that performs a controlled swap. It is universal for classical computation. It has the useful property that the numbers of 0s and 1s are conserved throughout, which in the billiard ball model means the same number of balls are output as input.Template:Anchor
Other named gates
| Names | # qubits | Operator symbol | Matrix | Circuit diagram | Properties | Named after | Refs |
|---|---|---|---|---|---|---|---|
| General single qubit rotation | 1 |
|
OpenQASM U gateTemplate:Efn | [11][25] | |||
| Template:Vanchor | 2 |
|
Adriano Barenco | [1] | |||
| Berkeley B | 2 |
|
University of California Berkeley[26] | [1] | |||
| Controlled-V,
controlled square root NOT |
2 | [9] | |||||
| Core entangling, canonical decomposition | 2 | , |
|
[1] | |||
| Dagwood Bumstead | 2 |
|
Comicbook Dagwood Bumstead[27] | [28][27] | |||
| Echoed cross resonance | 2 |
|
[29] | ||||
| Fermionic simulation | 2 | , |
|
[30][19][20] | |||
| Givens | 2 | , |
|
Givens rotations | [31] | ||
| Magic | 2 | [1] | |||||
| Sycamore | 2 | , | Google's Sycamore processor | [32] | |||
| CZ-SWAP | 2 | , |
|
[33] | |||
| Deutsch | 3 | , |
|
David Deutsch | [1] | ||
| Margolus, simplified Toffoli |
3 | , | 
|
|
Norman Margolus | [34][35] | |
| Peres | 3 | , | 
|
|
Asher Peres | [36] | |
| Toffoli, controlled-controlled NOT |
3 | 
|
|
Tommaso Toffoli | [1][6] | ||
Fermionic-Fredkin, Controlled-fermionic SWAP |
3 | ,
, |
[33] |
Notes
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 1.25 1.26 1.27 1.28 1.29 Template:Cite book
- ↑ Template:Cite web Qiskit online documentation.
- ↑ Template:Cite web Q# online documentation.
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ 6.00 6.01 6.02 6.03 6.04 6.05 6.06 6.07 6.08 6.09 6.10 6.11 6.12 6.13 6.14 6.15 Template:Cite book
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ 9.0 9.1 Template:Cite book
- ↑ Template:Cite book
- ↑ 11.0 11.1 11.2 11.3 Template:Cite book
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite web
- ↑ Template:Cite book
- ↑ Template:Cite web
- ↑ Template:Cite web
- ↑ 19.0 19.1 Template:Cite journal
- ↑ 20.0 20.1 Template:Cite journal
- ↑ Template:Citation
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ 27.0 27.1 Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ 33.0 33.1 Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite journal
- ↑ Template:Cite book
- ↑ Template:Cite journal
