Golden spiral

Golden spirals are self-similar. The shape is infinitely repeated when magnified.

In geometry, a golden spiral is a logarithmic spiral whose growth factor is Template:Math, the golden ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of Template:Math for every quarter turn it makes.

Approximations of the golden spiral

Approximate and true golden spirals: the green spiral is made from quarter-circles tangent to the interior of each square, while the red spiral is a golden spiral, a special type of logarithmic spiral. Overlapping portions appear yellow. The length of the side of a larger square to the next smaller square is in the golden ratio. For a square with side length 1, the next smaller square is Template:Nowrap wide. The next width is Template:Nowrap, then Template:Nowrap, and so on.

There are several comparable spirals that approximate, but do not exactly equal, a golden spiral.

For example, a golden spiral can be approximated by first starting with a rectangle for which the ratio between its length and width is the golden ratio. This rectangle can then be partitioned into a square and a similar rectangle and this rectangle can then be split in the same way. After continuing this process for an arbitrary number of steps, the result will be an almost complete partitioning of the rectangle into squares. The corners of these squares can be connected by quarter-circles. The result, though not a true logarithmic spiral, closely approximates a golden spiral.

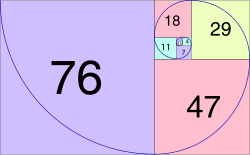
Another approximation is a Fibonacci spiral, which is constructed slightly differently. A Fibonacci spiral starts with a rectangle partitioned into 2 squares. In each step, a square the length of the rectangle's longest side is added to the rectangle. Since the ratio between consecutive Fibonacci numbers approaches the golden ratio as the Fibonacci numbers approach infinity, so too does this spiral get more similar to the previous approximation the more squares are added, as illustrated by the image.

Spirals in nature

It is sometimes erroneously stated that spiral galaxies and nautilus shells get wider in the pattern of a golden spiral, and hence are related to both Template:Math and the Fibonacci series. In truth, many mollusk shells including nautilus shells exhibit logarithmic spiral growth, but at a variety of angles usually distinctly different from that of the golden spiral. Although spiral galaxies have often been modeled as logarithmic spirals, Archimedean spirals, or hyperbolic spirals, their pitch angles vary with distance from the galactic center, unlike logarithmic spirals (for which this angle does not vary), and also at variance with the other mathematical spirals used to model them. Phyllotaxis, the pattern of plant growth, is in some case connected with the golden ratio because it involves successive leaves or petals being separated by the golden angle. Although this can sometimes be associated with spiral forms, such as in sunflower seed heads, these are more closely related to Fermat spirals than logarithmic spirals.

Mathematics

A Fibonacci spiral approximates the golden spiral using quarter-circle arcs inscribed in squares derived from the Fibonacci sequence.

A golden spiral with initial radius 1 is the locus of points of polar coordinates $(r,\theta )$ satisfying $$r={\phi }^{2\theta /\pi },$$ where $\phi$ is the golden ratio.

The polar equation for a golden spiral is the same as for other logarithmic spirals, but with a special value of the growth factor Template:Mvar: $$r=a{e}^{b\theta }$$ or $$\theta =\frac{1}{b}\ln (r/a),$$ with Template:Mvar being the base of natural logarithms, Template:Mvar being the initial radius of the spiral, and Template:Mvar such that when Template:Mvar is a right angle (a quarter turn in either direction): $$e^{b{\theta }_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}}=\phi .$$

Therefore, Template:Mvar is given by $$b=\frac{\ln \phi }{{\theta }_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}}.$$

The Lucas spiral approximates the golden spiral when its terms are large but not when they are small. 10 terms, from 2 to 76, are included.

The numerical value of Template:Mvar depends on whether the right angle is measured as 90 degrees or as $\frac{\pi }{2}$ radians; and since the angle can be in either direction, it is easiest to write the formula for the absolute value of Template:Mvar (that is, Template:Mvar can also be the negative of this value): $$|b|=\frac{\ln \phi }{90}\doteq 0.0053468$$ for Template:Mvar in degrees, or $$|b|=\frac{\ln \phi }{\pi /2}\doteq 0.3063489$$ for Template:Mvar in radians.

An alternate formula for a logarithmic and golden spiral is $$r=a{c}^{\theta }$$ where the constant Template:Mvar is given by $$c=e^b$$ which for the golden spiral gives Template:Mvar values of $$c={\phi }^{\frac{1}{90}}\doteq 1.0053611$$ if Template:Mvar is measured in degrees, and $$c={\phi }^{\frac{2}{\pi }}\doteq 1.358456$$ if Template:Mvar is measured in radians.

With respect to logarithmic spirals the golden spiral has the distinguishing property that for four collinear spiral points A, B, C, D belonging to arguments Template:Math, Template:Math, Template:Math, Template:Math the point C is the projective harmonic conjugate of B with respect to A, D, i.e. the cross ratio (A,D;B,C) has the singular value −1. The golden spiral is the only logarithmic spiral with (A,D;B,C) = (A,D;C,B).

Polar slope

Definition of slope angle and sector

In the polar equation for a logarithmic spiral: $$r=a{e}^{b\theta }$$ the parameter Template:Mvar is related to the polar slope angle $\alpha$: $$\tan \alpha =b.$$

In a golden spiral, $b$ being constant and equal to $|b|=\frac{\ln \phi }{\pi /2}$ (for Template:Mvar in radians, as defined above), the slope angle $\alpha$ is $$\alpha =\arctan (|b|)=\arctan \left(\frac{\ln \phi }{\pi /2}\right),$$ hence $$\alpha \doteq 17.03239113$$ if measured in degrees, or $$\alpha \doteq 0.2972713047$$ if measured in radians.

Its complementary angle $$\beta =\pi /2-\alpha \doteq 1.273525022$$ in radians, or $$\beta =90-\alpha \doteq 73$$ in degrees, is the angle the golden spiral arms make with a line from the center of the spiral.

See also

• Fibonacci sequence
• Golden angle
• Golden ratio
• Golden rectangle
• List of spirals
• Logarithmic spiral