Periodic summation

A Fourier transform and 3 variations caused by periodic sampling (at interval T) and/or periodic summation (at interval P) of the underlying time-domain function.

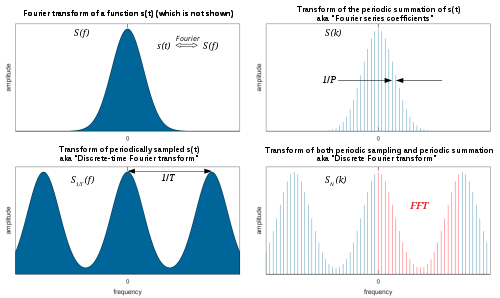
In mathematics, any integrable function $s(t)$ can be made into a periodic function $s_P(t)$ with period P by summing the translations of the function $s(t)$ by integer multiples of P. This is called periodic summation:

$s_P(t)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}s(t+nP)$

When $s_P(t)$ is alternatively represented as a Fourier series, the Fourier coefficients are equal to the values of the continuous Fourier transform, $S(f)\triangleq ℱ\{s(t)\},$ at intervals of $\frac{1}{P}$. That identity is a form of the Poisson summation formula. Similarly, a Fourier series whose coefficients are samples of $s(t)$ at constant intervals (T) is equivalent to a periodic summation of $S(f),$ which is known as a discrete-time Fourier transform.

The periodic summation of a Dirac delta function is the Dirac comb. Likewise, the periodic summation of an integrable function is its convolution with the Dirac comb.

Quotient space as domain

If a periodic function is instead represented using the quotient space domain $ℝ/(P\mathbb{Z})$ then one can write:

${\phi }_P:ℝ/(P\mathbb{Z})\to ℝ$

${\phi }_P(x)=\sum _{\tau \in x}s(\tau ).$

The arguments of ${\phi }_P$ are equivalence classes of real numbers that share the same fractional part when divided by $P$.

See also

• Dirac comb
• Circular convolution
• Discrete-time Fourier transform