Circle packing in a square: Difference between revisions
(No difference)
|
Latest revision as of 18:22, 30 December 2024
Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack Template:Mvar unit circles into the smallest possible square. Equivalently, the problem is to arrange Template:Mvar points in a unit square aiming to get the greatest minimal separation, Template:Mvar, between points.[1] To convert between these two formulations of the problem, the square side for unit circles will be Template:Math.
Solutions
Solutions (not necessarily optimal) have been computed for every Template:Math.[2] Solutions up to Template:Math are shown below.[2] The obvious square packing is optimal for 1, 4, 9, 16, 25, and 36 circles (the six smallest square numbers), but ceases to be optimal for larger squares from 49 onwards.[2]
| Number of circles (Template:Mvar) | Square side length (Template:Mvar) | Template:Mvar[1] | Number density (Template:Math) | Figure |
|---|---|---|---|---|
| 1 | 2 | ∞ | 0.25 | |
| 2 | ≈ 3.414... |
≈ 1.414... |
0.172... | 
|
| 3 | ≈ 3.931... |
≈ 1.035... |
0.194... | 
|
| 4 | 4 | 1 | 0.25 | 
|
| 5 | ≈ 4.828... |
≈ 0.707... |
0.215... | 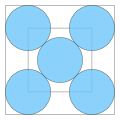
|
| 6 | ≈ 5.328... |
≈ 0.601... |
0.211... | 
|
| 7 | ≈ 5.732... |
≈ 0.536... |
0.213... | 
|
| 8 | ≈ 5.863... |
≈ 0.518... |
0.233... | 
|
| 9 | 6 | 0.5 | 0.25 | 
|
| 10 | 6.747... | 0.421... Template:OEIS2C | 0.220... | 
|
| 11 | ≈ 7.022... |
0.398... | 0.223... | 
|
| 12 | ≈ 7.144... |
≈ 0.389... |
0.235... | 
|
| 13 | 7.463... | 0.366... | 0.233... | 
|
| 14 | ≈ 7.732... |
≈ 0.349... |
0.226... | 
|
| 15 | ≈ 7.863... |
≈ 0.341... |
0.243... | 
|
| 16 | 8 | 0.333... | 0.25 | 
|
| 17 | 8.532... | 0.306... | 0.234... | 
|
| 18 | ≈ 8.656... |
≈ 0.300... |
0.240... | 
|
| 19 | 8.907... | 0.290... | 0.240... | 
|
| 20 | ≈ 8.978... |
≈ 0.287... |
0.248... | 
|
Circle packing in a rectangle
Dense packings of circles in non-square rectangles have also been the subject of investigations.[3][4]