Fixed-point iteration

Template:Short description Template:Refimprove In numerical analysis, fixed-point iteration is a method of computing fixed points of a function.

More specifically, given a function $f$ defined on the real numbers with real values and given a point $x_0$ in the domain of $f$, the fixed-point iteration is $$x_{n+1}=f(x_n),n=0,1,2,\dots$$ which gives rise to the sequence $x_0,x_1,x_2,\dots$ of iterated function applications $x_0,f(x_0),f(f(x_0)),\dots$ which is hoped to converge to a point $x_{\text{fix}}$. If $f$ is continuous, then one can prove that the obtained $x_{\text{fix}}$ is a fixed point of $f$, i.e., $$f(x_{\text{fix}})=x_{\text{fix}}.$$

More generally, the function $f$ can be defined on any metric space with values in that same space.

Examples

The fixed-point iteration Template:Math with initial value Template:Math converges to 0. This example does not satisfy the assumptions of the Banach fixed-point theorem and so its speed of convergence is very slow.

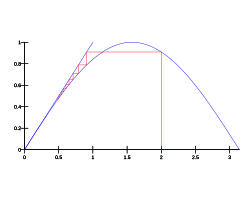
• A first simple and useful example is the Babylonian method for computing the square root of Template:Math, which consists in taking $f(x)=\frac{1}{2}(\frac{a}{x}+x)$, i.e. the mean value of Template:Mvar and Template:Math, to approach the limit $x=\sqrt{a}$ (from whatever starting point $x_0\gg 0$). This is a special case of Newton's method quoted below.
• The fixed-point iteration $x_{n+1}=\cos x_n$ converges to the unique fixed point of the function $f(x)=\cos x$ for any starting point $x_0.$ This example does satisfy (at the latest after the first iteration step) the assumptions of the Banach fixed-point theorem. Hence, the error after n steps satisfies $|x_n-x|\le \frac{q^n}{1-q}|x_1-x_0|=C{q}^n$ (where we can take $q=0.85$, if we start from $x_0=1$.) When the error is less than a multiple of $q^n$ for some constant Template:Math, we say that we have linear convergence. The Banach fixed-point theorem allows one to obtain fixed-point iterations with linear convergence.
• The requirement that Template:Math is continuous is important, as the following example shows. The iteration $$x_{n+1}=\{\begin{array}{cc}\frac{x_n}{2},& x_n\ne 0\\ 1,& x_n=0\end{array}$$ converges to 0 for all values of $x_0$. However, 0 is not a fixed point of the function $$f(x)=\{\begin{array}{cc}\frac{x}{2},& x\ne 0\\ 1,& x=0\end{array}$$ as this function is not continuous at $x=0$, and in fact has no fixed points.

Attracting fixed points

The fixed point iteration Template:Math with initial value Template:Math.

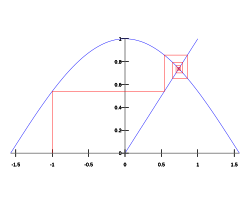
An attracting fixed point of a function Template:Math is a fixed point Template:Math of Template:Math with a neighborhood Template:Math of "close enough" points around Template:Math such that for any value of Template:Mvar in Template:Math, the fixed-point iteration sequence $$x,f(x),f(f(x)),f(f(f(x))),\dots$$ is contained in Template:Math and converges to Template:Math. The basin of attraction of Template:Math is the largest such neighborhood Template:Math.

The natural cosine function ("natural" means in radians, not degrees or other units) has exactly one fixed point, and that fixed point is attracting. In this case, "close enough" is not a stringent criterion at all—to demonstrate this, start with any real number and repeatedly press the cos key on a calculator (checking first that the calculator is in "radians" mode). It eventually converges to the Dottie number (about 0.739085133), which is a fixed point. That is where the graph of the cosine function intersects the line $y=x$.

Not all fixed points are attracting. For example, 0 is a fixed point of the function Template:Math, but iteration of this function for any value other than zero rapidly diverges. We say that the fixed point of $f(x)=2x$ is repelling.

An attracting fixed point is said to be a stable fixed point if it is also Lyapunov stable.

A fixed point is said to be a neutrally stable fixed point if it is Lyapunov stable but not attracting. The center of a linear homogeneous differential equation of the second order is an example of a neutrally stable fixed point.

Multiple attracting points can be collected in an attracting fixed set.

Banach fixed-point theorem

The Banach fixed-point theorem gives a sufficient condition for the existence of attracting fixed points. A contraction mapping function $f$ defined on a complete metric space has precisely one fixed point, and the fixed-point iteration is attracted towards that fixed point for any initial guess $x_0$ in the domain of the function. Common special cases are that (1) $f$ is defined on the real line with real values and is Lipschitz continuous with Lipschitz constant $L<1$, and (2) the function Template:Math is continuously differentiable in an open neighbourhood of a fixed point Template:Math, and $|f^{\prime }(x_{\text{fix}})|<1$.

Although there are other fixed-point theorems, this one in particular is very useful because not all fixed-points are attractive. When constructing a fixed-point iteration, it is very important to make sure it converges to the fixed point. We can usually use the Banach fixed-point theorem to show that the fixed point is attractive.

Attractors

Attracting fixed points are a special case of a wider mathematical concept of attractors. Fixed-point iterations are a discrete dynamical system on one variable. Bifurcation theory studies dynamical systems and classifies various behaviors such as attracting fixed points, periodic orbits, or strange attractors. An example system is the logistic map.

Iterative methods

In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the n-th approximation is derived from the previous ones. Convergent fixed-point iterations are mathematically rigorous formalizations of iterative methods.

Convergence acceleration

The speed of convergence of the iteration sequence can be increased by using a convergence acceleration method such as Anderson acceleration and Aitken's delta-squared process. The application of Aitken's method to fixed-point iteration is known as Steffensen's method, and it can be shown that Steffensen's method yields a rate of convergence that is at least quadratic.

Chaos game

Sierpinski triangle created using IFS, selecting all members at each iteration

The term chaos game refers to a method of generating the fixed point of any iterated function system (IFS). Starting with any point Template:Math, successive iterations are formed as Template:Math, where Template:Math is a member of the given IFS randomly selected for each iteration. Hence the chaos game is a randomized fixed-point iteration. The chaos game allows plotting the general shape of a fractal such as the Sierpinski triangle by repeating the iterative process a large number of times. More mathematically, the iterations converge to the fixed point of the IFS. Whenever Template:Math belongs to the attractor of the IFS, all iterations Template:Math stay inside the attractor and, with probability 1, form a dense set in the latter.

See also

• Fixed-point combinator
• Cobweb plot
• Markov chain
• Infinite compositions of analytic functions
• Rate of convergence

Further reading

• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite book
• Template:Cite journal

External links

• Fixed-point algorithms online
• Fixed-point iteration online calculator (Mathematical Assistant on Web)