Infinite dihedral group

p1m1, (*∞∞)	p2, (22∞)	p2mg, (2*∞)
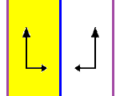
In 2-dimensions three frieze groups p1m1, p2, and p2mg are isomorphic to the Dih∞ group. They all have 2 generators. The first has two parallel reflection lines, the second two 2-fold gyrations, and the last has one mirror and one 2-fold gyration.

In one dimension, the infinite dihedral group is seen in the symmetry of an apeirogon alternating two edge lengths, containing reflection points at the center of each edge.

In mathematics, the infinite dihedral group Dih_∞ is an infinite group with properties analogous to those of the finite dihedral groups.

In two-dimensional geometry, the infinite dihedral group represents the frieze group symmetry, p1m1, seen as an infinite set of parallel reflections along an axis.

Definition

Every dihedral group is generated by a rotation r and a reflection; if the rotation is a rational multiple of a full rotation, then there is some integer n such that rⁿ is the identity, and we have a finite dihedral group of order 2n. If the rotation is not a rational multiple of a full rotation, then there is no such n and the resulting group has infinitely many elements and is called Dih_∞. It has presentations

$⟨r,s\mid s^2=1,srs=r^{-1}⟩$

$⟨x,y\mid x^2=y^2=1⟩$

and is isomorphic to a semidirect product of Z and Z/2, and to the free product Z/2 * Z/2. It is the automorphism group of the graph consisting of a path infinite to both sides. Correspondingly, it is the isometry group of Z (see also symmetry groups in one dimension), the group of permutations α: Z → Z satisfying |i − j| = |α(i) − α(j)|, for all i, j in Z.

The infinite dihedral group can also be defined as the holomorph of the infinite cyclic group.

Aliasing

When periodically sampling a sinusoidal function at rate Template:Math, the abscissa above represents its frequency, and the ordinate represents another sinusoid that could produce the same set of samples. An infinite number of abscissas have the same ordinate (an equivalence class with the fundamental domain Template:Math), and they exhibit dihedral symmetry. The many-to-one phenomenon is known as aliasing.

Template:Details An example of infinite dihedral symmetry is in aliasing of real-valued signals.

When sampling a function at frequency Template:Math (intervals Template:Math), the following functions yield identical sets of samples: Template:Math}. Thus, the detected value of frequency Template:Mvar is periodic, which gives the translation element Template:Math. The functions and their frequencies are said to be aliases of each other. Noting the trigonometric identity:

$\sin (2\pi (f+N{f}_s)t+\phi )=\{\begin{array}{cc}+\sin (2\pi (f+N{f}_s)t+\phi ),& f+N{f}_s\ge 0,\\ -\sin (2\pi |f+N{f}_s|t-\phi ),& f+N{f}_s<0,\end{array}$

we can write all the alias frequencies as positive values: $|f+N{f}_s|$. This gives the reflection (Template:Mvar) element, namely Template:Mvar ↦ Template:Mvar.  For example, with Template:Math  and  Template:Math,  Template:Math  reflects to  Template:Math, resulting in the two left-most black dots in the figure.  The other two dots correspond to Template:Math  and  Template:Math. As the figure depicts, there are reflection symmetries, at 0.5Template:Math,  Template:Math,  1.5Template:Math,  etc.  Formally, the quotient under aliasing is the orbifold [0, 0.5Template:Math], with a Z/2 action at the endpoints (the orbifold points), corresponding to reflection.

See also

• The orthogonal group O(2), another infinite generalization of the finite dihedral groups
• The affine symmetric group, a family of groups including the infinite dihedral group